题目内容
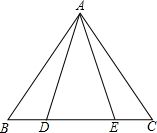 如图,已知D,E是△ABC中BC边上的两点,且AD=AE,请你再添加一个条件:
如图,已知D,E是△ABC中BC边上的两点,且AD=AE,请你再添加一个条件:考点:全等三角形的判定
专题:开放型
分析:根据等腰三角形性质求出∠ADE=∠AED,推出∠ADB=∠AEC,根据全等三角形的判定推出即可.
解答:解:BD=EC,
理由是:∵AD=AE,
∴∠ADE=∠AED,
∵∠ADE+∠ADB=180°,∠AED+∠AEC=180°,
∴∠ADB=∠AEC,
在△ABD和△ACE中
∴△ABD≌△ACE
故答案为:BD=EC.
理由是:∵AD=AE,
∴∠ADE=∠AED,
∵∠ADE+∠ADB=180°,∠AED+∠AEC=180°,
∴∠ADB=∠AEC,
在△ABD和△ACE中
|
∴△ABD≌△ACE
故答案为:BD=EC.
点评:本题考查了等腰三角形的性质,全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,此题是一道开放型的题目,答案不唯一.

练习册系列答案
相关题目
下面的单项式中次数与另外单项式次数不同的是( )
A、
| ||
| B、-3xy2z | ||
| C、πxy2 | ||
| D、32xy3 |
如果有理数a,b在数轴上对应的点分别在原点的左、右两侧,那么(|a|+b)÷(a-b)的符号是( )
| A、正号 | B、负号 |
| C、正号或负号 | D、0 |
若a,b是有理数,且
=0,则( )
| a |
| b |
| A、a=0且b≠0 |
| B、a=0 |
| C、a=0或b=0 |
| D、a,b同号 |
 如图,在平面直角坐标系中,过点C(0,4)的直线l1与过点O的直线l2交于点B(2
如图,在平面直角坐标系中,过点C(0,4)的直线l1与过点O的直线l2交于点B(2 如图,已知:在?ABCD中,AC为对角线,DE交AC于F,交AB于E,AE:EB=1:2,S△AEF=5,求S△CDF的值.
如图,已知:在?ABCD中,AC为对角线,DE交AC于F,交AB于E,AE:EB=1:2,S△AEF=5,求S△CDF的值.