题目内容
如果有理数a,b在数轴上对应的点分别在原点的左、右两侧,那么(|a|+b)÷(a-b)的符号是( )
| A、正号 | B、负号 |
| C、正号或负号 | D、0 |
考点:有理数的混合运算,数轴
专题:
分析:由数轴可得a<0<b,分别得到|a|+b>0,a-b<0,进一步即可得出结论.
解答:解:∵有理数a,b在数轴上对应的点分别在原点的左、右两侧,
∴a<0<b,
∴|a|+b>0,a-b<0,
∴(|a|+b)÷(a-b)<0.
故(|a|+b)÷(a-b)的符号是负号.
故选:B.
∴a<0<b,
∴|a|+b>0,a-b<0,
∴(|a|+b)÷(a-b)<0.
故(|a|+b)÷(a-b)的符号是负号.
故选:B.
点评:本题主要考查了有理数的混合运算,数轴,解题的关键是记住数轴上数的特点,得到|a|+b>0,a-b<0.

练习册系列答案
相关题目
下列计算正确的是( )
| A、x4•x3=x12 |
| B、y3•y3=2y3 |
| C、x4+x4=x8 |
| D、x9•x=x10 |
下列说法中正确的是( )
| A、不是正数的数一定是负数,不是负数的数一定是正数 |
| B、符号相反的数互为相反数 |
| C、一个数的绝对值越大,表示它的点在数轴上离原点越远 |
| D、如果a大于b,那么a的倒数小于b的倒数 |
 如图,正方形卡片A类、B类和长方形卡片C类各若干张,若要拼一个长为(3a+b)的大正方形,则需要C类卡片张数是( )
如图,正方形卡片A类、B类和长方形卡片C类各若干张,若要拼一个长为(3a+b)的大正方形,则需要C类卡片张数是( ) 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=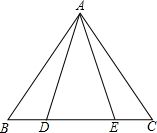 如图,已知D,E是△ABC中BC边上的两点,且AD=AE,请你再添加一个条件:
如图,已知D,E是△ABC中BC边上的两点,且AD=AE,请你再添加一个条件: