Question

16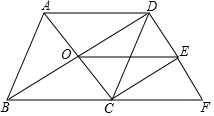．如图，点O是菱形ABCD对角线的交点，DF∥AC交BC的延长线于点F，CE∥BD交DF于点E，连接OE．
（1）求证：四边形OCED是矩形；
（2）当AB=5，AC=6时，求△BDF的周长．

Answer 1

分析 （1）易证四边形OCED是平行四边形，再根据菱形的性质可得∠COD=90°，进而可证明四边形OCED是矩形；
（2）首先证明四边形ACFD是平行四边形，所以可得AC=DF，再证明△BDF是直角三角形，由勾股定理可求出BD的长，进而可求出△BDF的周长．

解答 解：
（1）证明：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
又∵四边形ABCD是，
∴AC⊥BD，
即∠COD=90°，
∴四边形OCED是矩形；
（2）∵四边形ABCD是菱形，
∴AD=BC=AB=DC，AD∥BC，AC⊥BD，
∵AC∥DF，
∴四边形ACFD是平行四边形，
∴AC=DF=6，AD=CF=5，
∴BF=BC+AD=10
∵AC∥DF，
∴∠BOC=∠BDF=90°，
∴BD=$\sqrt{B{F}^{2}-D{F}^{2}}$=8，
∴△BDF的周长=8+6+10=24．

点评 本题考查了菱形的性质、平行四边形的判断和性质、矩形的判断和性质以及勾股定理的运用，证明△BDF是直角三角形是解题的关键．