题目内容
15.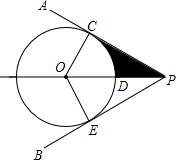 如图,点O在∠APB的平分线上,⊙O与PA相切于点C,PO与⊙O相交点D,PO=2,若D为PO的中点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{1}{6}$π.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C,PO与⊙O相交点D,PO=2,若D为PO的中点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{1}{6}$π.
分析 首先连接DC,由CP与⊙O相切于C,可得OC⊥CP,根据直角三角形斜边中线的性质得出OC=OD=CD=1,从而得出△COD是等边三角形,得出∠COD=60°,然后根据勾股定理求得PC的长,然后由S阴影=S△COP-S扇形DOC,即可求得答案.
解答 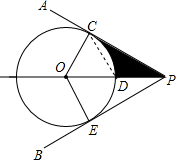 解:连接CD,
解:连接CD,
∵CP与⊙O相切于C,
∴OC⊥CP,
∵PO=2,若D为PO的中点,
∴OC=OD=CD=1,
∴△COD是等边三角形,
∴∠COD=60°,
∵OC=1,OP=2,
∴PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=$\sqrt{3}$,
∴S阴影=S△COP-S扇形DOC=$\frac{1}{2}$×$\sqrt{3}×1$-$\frac{60π×{1}^{2}}{360}$=$\frac{\sqrt{3}}{2}$-$\frac{1}{6}$π.
故答案为$\frac{\sqrt{3}}{2}$-$\frac{1}{6}$π.
点评 此题考查了切线的性质、勾股定理、扇形的面积以及直角三角形斜边中线的性质.此题难度适中.

练习册系列答案
相关题目
5.在二次函数y=-$\frac{1}{12}$(x-2)2+3的图象上有两点(-1,y1),(1,y2),则y1-y2的值是( )
| A. | 负数 | B. | 零 | C. | 正数 | D. | 不能确定 |
6.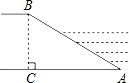 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(| A. | 15m | B. | 20$\sqrt{3}$m | C. | 20m | D. | 10$\sqrt{3}$m |
3.下列实数中,最大的是( )
| A. | -1 | B. | -2 | C. | -$\sqrt{2}$ | D. | -$\frac{4}{3}$ |
20.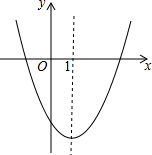 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:①b2>4ac;②4a-2b+c<0;③b<-2c;④若点(-2,y1)与(5,y2)是抛物线上的两点,则y1<y2,其中,正确的结论是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:①b2>4ac;②4a-2b+c<0;③b<-2c;④若点(-2,y1)与(5,y2)是抛物线上的两点,则y1<y2,其中,正确的结论是( )
 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:①b2>4ac;②4a-2b+c<0;③b<-2c;④若点(-2,y1)与(5,y2)是抛物线上的两点,则y1<y2,其中,正确的结论是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:①b2>4ac;②4a-2b+c<0;③b<-2c;④若点(-2,y1)与(5,y2)是抛物线上的两点,则y1<y2,其中,正确的结论是( )| A. | ①② | B. | ①③ | C. | ①③④ | D. | ②③④ |
4.若一个三角形的外心在这个三角形的一边上,那么这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
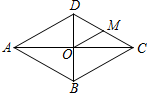 如图,在菱形ABCD中,对角线AC与BD相交于点O,点M是CD边的中点,连结OM,若OM=$\frac{5}{2}$cm,则菱形ABCD的周长为20cm.
如图,在菱形ABCD中,对角线AC与BD相交于点O,点M是CD边的中点,连结OM,若OM=$\frac{5}{2}$cm,则菱形ABCD的周长为20cm.