题目内容
17.有这样一道题:“计算:$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$÷$\frac{x-1}{{x}^{2}+x}$-x的值,其中x=2004.”甲同学把“x=2004”错抄成“x=2040”,但他的计算结果也是正确的.你说这是怎么回事?分析 将分式的分子、分母因式分解,除法化为乘法,约分,再代值计算,代值时,x的取值不能使得原式的分母,除式为0.
解答 解:∵$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$÷$\frac{x-1}{{x}^{2}+x}$-x=$\frac{(x-1)^{2}}{(x-1)(x+1)}$•$\frac{x-1}{x(x+1)}$-x=x-x=0,
∴无论x等于什么数原式的值都是定值0,
∴甲同学把“x=2004”错抄成“x=2040”,其结果都是0,即他的计算结果也是正确的.
点评 本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
12.下列计算正确的是( )
| A. | (m+n)2=m2+n2 | B. | m2•m3=m5 | C. | 2m+3n=5mn | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3 |
12.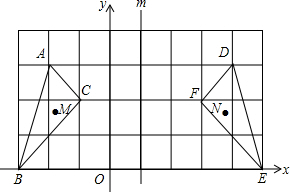 如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
 如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )| A. | -a | B. | -a+1 | C. | a+2 | D. | -a+2 |
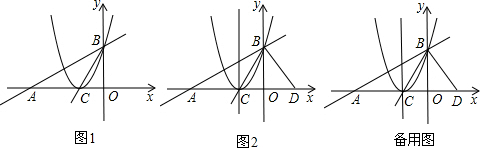
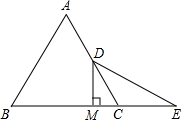 如图,△ABC是等边三角形,点E是BC延长线上的点,BE的垂直平分线交AC于点D,垂足为M,CE=CD,求证:AD=CD.
如图,△ABC是等边三角形,点E是BC延长线上的点,BE的垂直平分线交AC于点D,垂足为M,CE=CD,求证:AD=CD.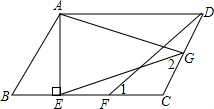 已知:在?ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知:在?ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.