题目内容

20．若m=$\root{5x+6y-11}{x-2y}$表示x-2y的算术平方根，n=$\root{7x+18y+1}{y-{x}^{2}}$表示y-x2的立方根，求m3-n2+1的立方根．

分析 利用算术平方根、立方根的定义求出x与y的值，进而确定出m与n的值，代入原式计算即可求出立方根．

解答 解：由题意得：$\left\{\begin{array}{l}{5x+6y=13}\\{7x+18y=-1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=5}\\{y=-2}\end{array}\right.$，
∴m=3，n=-3，
∴m3-n2+1=27-9+1=19，即19的立方根为$\root{3}{19}$．

点评 此题考查了立方根，以及算术平方根，熟练掌握各自的定义是解本题的关键．

练习册系列答案
相关题目
10．下列说法错误的个数是（　　）
①同位角相等； 
②过一点有且只有一条直线与已知直线垂直；
③过一点有且只有一条直线与已知直线平行； 
④若a∥b，b∥c，则a∥c．
A．、1个B．2个C．3个D．4个
11．某超市出售的品牌月饼袋上，分别标有质量为（500±5）g，它们的质量最多相差（　　）
A．10gB．20gC．30gD．40g
8．若二次函数y=x2-6x+c的图象过A（-1，y1），B（3，y2），C（3+$\sqrt{2}$，y3），则y1，y2，y3的大小关系是（　　）
A．y1＞y2＞y3B．y1＞y3＞y2C．y2＞y1＞y3D．y3＞y1＞y2
15．计算：
（1）（-1）2016-（-9）+$\sqrt{16}$；
（2）$\sqrt{64}$+$\root{3}{-8}$+$\sqrt{\frac{4}{25}}$．
5．（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．
填空：①∠AEB的度数为60°；②线段AD、BE之间的数量关系是AD=BE．试证明你的结论．
（2）拓展研究：
如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，若AE=15，DE=9，求BE的长度．
（3）探究发现：
图1中的△ACB和△DCE，在△DCE旋转过程中当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．
12．已知：AB为⊙O直径，M、N是⊙O上的两点，且$\sqrt{2}$BM=2OB．
（1）如图1，求证：∠N=45°；
（2）如图2，若AN∥BM，C为弧AM上一点，连接CN、OC，CN与AO交于点D，若OD=CD，求证：CN=$\sqrt{3}$OB；
（3）在（2）的条件下，如图3，P为BM上的一点，若OD=$\sqrt{2}$，BP=2，求PC的长．
9．如图，已知点D是AB边的中点，AF∥BC，CG：GA=3：1，BC=8，则AF等于（　　）
A．2B．4C．16D．8
10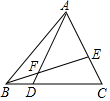．D、E分别为△ABC中BC、AC边上的点，且BD：DC=1：3，AE：EC=2：1，则AF：FD=（　　）
A．3：1B．5：1C．8：1D．9：1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网