题目内容
9.下列长度的各组线段:①9,12,15;②7,24,25;③$\frac{3}{4}$,1,$\frac{5}{4}$;④3a,4a,5a(a>0)其中可以构成直角三角形的有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答 解:①∵92+122=152,∴可以构成直角三角形;
②∵72+242=252,∴可以构成直角三角形;
③∵($\frac{3}{4}$)2+12=($\frac{5}{4}$)2,∴可以构成直角三角形;
④∵(3a)2+(4a)2=(5a)2,∴可以构成直角三角形;
共4组,
故选:D.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
19.抛物线y=3x2+2x的开口方向是( )
| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
20.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 抛物线与x轴的一个交点为(4,0) | B. | 函数y=ax2+bx+c的最大值为6 | ||
| C. | 抛物线的对称轴是x=$\frac{1}{2}$ | D. | 在对称轴右侧,y随x增大而增大 |
17.已知抛物线y=ax2+2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
1.已知平面上有一点P和半径为r的⊙O,OP=d,d与r是关于x的方程x2-7x+12=0的两根,则点P与⊙O的位置关系是( )
| A. | 点P在圆外 | B. | 点P在圆内 | ||
| C. | 点P不在圆上 | D. | 点P在圆外或点P在圆内 |
18.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,10 | C. | 2,3,4 | D. | 1,1,2 |
19.下列多项式:①x2+y2;②x2-1;③x3+4x-4;④x2-10x+25,其中能直接用公式法因式分解的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 在Rt△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.问△AEF与△DEB全等吗?说明理由.
在Rt△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.问△AEF与△DEB全等吗?说明理由.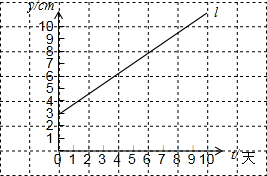 如图,某植物t天后的高度为ycm,l放映了y与t之间的关系,根据图象回答下列问题:
如图,某植物t天后的高度为ycm,l放映了y与t之间的关系,根据图象回答下列问题: