题目内容
 如图,OQ是∠AOB的平分线,P是OQ上一点,PC⊥OA于C交OB于E,PD⊥OB交OA于F,求证:DE=CF.
如图,OQ是∠AOB的平分线,P是OQ上一点,PC⊥OA于C交OB于E,PD⊥OB交OA于F,求证:DE=CF.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:如图,证明PC=PD,此为解题的关键;证明△PDE≌△PCF,即可解决问题.
解答: 解:如图,∵OQ是∠AOB的平分线,PC⊥OA,PD⊥OB,
解:如图,∵OQ是∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD;在△PDE与△PCF中,
,
∴△PDE≌△PCF(ASA),
∴DE=CF.
 解:如图,∵OQ是∠AOB的平分线,PC⊥OA,PD⊥OB,
解:如图,∵OQ是∠AOB的平分线,PC⊥OA,PD⊥OB,∴PC=PD;在△PDE与△PCF中,
|
∴△PDE≌△PCF(ASA),
∴DE=CF.
点评:该题主要考查了角平分线的性质、全等三角形的判定及其性质的应用问题;灵活运用角平分线的性质、全等三角形的判定来分析、解答是解题的关键.

练习册系列答案
相关题目
 如图所示,已知在半径是3cm的⊙O中,弧AB的长为
如图所示,已知在半径是3cm的⊙O中,弧AB的长为 如图,AB,AD,DC与半圆O均相切,AD∥BC,AB=8,CD=5,则BC=
如图,AB,AD,DC与半圆O均相切,AD∥BC,AB=8,CD=5,则BC= 如图所示,∠3+∠4=180°,则∠1
如图所示,∠3+∠4=180°,则∠1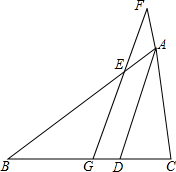 △ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=
△ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=