题目内容
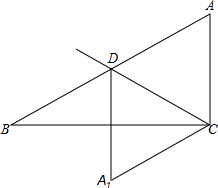 已知,如图,在△ABC中,∠C=90°,过点C的射线交AB于D,将△ACD沿射线CD翻折得到△A1CD,A1D⊥BC,求证:△ACD为等腰三角形.
已知,如图,在△ABC中,∠C=90°,过点C的射线交AB于D,将△ACD沿射线CD翻折得到△A1CD,A1D⊥BC,求证:△ACD为等腰三角形.考点:翻折变换(折叠问题)
专题:证明题
分析:首先根据题意证明A1D∥AC,进而证明∠A1DC=∠ACD;利用对称变换的性质证明∠ADC=∠A1DC,即可解决问题.
解答: 解:如图,
解:如图,
∵∠C=90°,A1D⊥BC
∴A1D∥AC,
∴∠A1DC=∠ACD;
又∵△ACD≌△A1CD,
∴∠ADC=∠A1DC,
∴∠ADC=∠ACD,
∴AD=CD,
即△ACD为等腰三角形.
 解:如图,
解:如图,∵∠C=90°,A1D⊥BC
∴A1D∥AC,
∴∠A1DC=∠ACD;
又∵△ACD≌△A1CD,
∴∠ADC=∠A1DC,
∴∠ADC=∠ACD,
∴AD=CD,
即△ACD为等腰三角形.
点评:该命题以三角形为载体,借助对称变换考查了平行线的性质、全等三角形的性质等几何知识点;对分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目

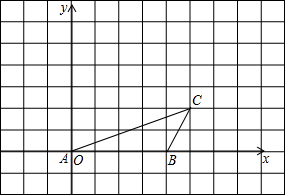 如图,已知点A、B、C的坐标分别为(0,0),(4,0),(5,2).将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A、B、C的坐标分别为(0,0),(4,0),(5,2).将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.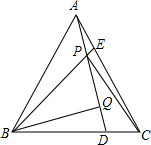 如图,D、E分别在正△ABC的边BC和AC上,且AE=CD,连BE交AD于P,过点B作BQ⊥AD于点Q.
如图,D、E分别在正△ABC的边BC和AC上,且AE=CD,连BE交AD于P,过点B作BQ⊥AD于点Q.