题目内容
9.已知△ABC为等边三角形,以AB为斜边作Rt△ADB,∠ADB=90°,AD=1且∠ABD=15°,则点C到BD的距离为$2+\sqrt{3}$.分析 根据等边三角形的性质和全等三角形的判定和性质进行解答即可.
解答 解:如图:过点C作CE⊥BD,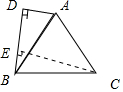
∵△ABC为等边三角形,
∴AB=BC,∠ABC=60°,
∵∠ABD=15°,
∴∠BCE=90°-60°-15°=15°,
在△ADB与△CBE中,
$\left\{\begin{array}{l}{∠ADB=∠CEB=90°}\\{∠ABD=∠ECB=15°}\\{AB=BC}\end{array}\right.$,
∴△ADB≌△CBE(AAS),
∴CE=BD=$\frac{AD}{tan15°}=\frac{1}{2-\sqrt{3}}=2+\sqrt{3}$,
故答案为:$2+\sqrt{3}$.
点评 此题考查等边三角形的性质,关键是根据等边三角形的性质和全等三角形的判定和性质解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知一组数据中,前5个数的平均数是a,后6个数的平均数是b,则这组数据的平均数是( )
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
4.下列说法正确的是( )
| A. | 飞机上升9000米,再上升-5000米,则飞机实际上升4000米 | |
| B. | 一个正数,一个负数,它们表示的意义一定相反 | |
| C. | 0是最小的有理数 | |
| D. | 正数和负数统称为有理数 |
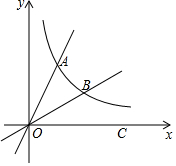 如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.
如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.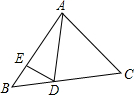 如图,△ABC中,D、E分别是BC、AB边上的点,AD平分∠EDC,试说明∠BED>∠B的道理.
如图,△ABC中,D、E分别是BC、AB边上的点,AD平分∠EDC,试说明∠BED>∠B的道理.