题目内容
 如图,直角三角形△ABC中,∠ACB=90°,∠ABC=60°,BD=2CD,CF⊥AD于E,AF-BF=16,则AB=________.
如图,直角三角形△ABC中,∠ACB=90°,∠ABC=60°,BD=2CD,CF⊥AD于E,AF-BF=16,则AB=________.
20
分析:作GD∥AB,交CF于G点,设DG=x,则BF=3x.再考虑用x表示AF,关键是求出AE:ED的比值,由相似关系或射影定理可以得到:AC2=AE•AD,CD2=DE•AD,则AE:ED=AC2:CD2=27:1,所以AF=27x,从而得出AB.
解答: 解:作GD∥AB,交CF于G点,
解:作GD∥AB,交CF于G点,
设DG=x,则BF=3x.
∵CF⊥AD,
∴∠AEC=90°,
∵∠ACB=90°,
∴△AEC∽△ACD∽△CED,
∴AC2=AE•AD,CD2=DE•AD,
∴AE:ED=AC2:CD2=27:1
∴AF=27x,
∵AF-BF=16,
∴27x-3x=24x=16,
∴x= ,
,
∴AB=AF+BF=3x+27x=30x=30× =20.
=20.
点评:本题考查了全等三角形的判定和性质以及直角三角形的性质,是基础知识要熟练掌握.
分析:作GD∥AB,交CF于G点,设DG=x,则BF=3x.再考虑用x表示AF,关键是求出AE:ED的比值,由相似关系或射影定理可以得到:AC2=AE•AD,CD2=DE•AD,则AE:ED=AC2:CD2=27:1,所以AF=27x,从而得出AB.
解答:
 解:作GD∥AB,交CF于G点,
解:作GD∥AB,交CF于G点,设DG=x,则BF=3x.
∵CF⊥AD,
∴∠AEC=90°,
∵∠ACB=90°,
∴△AEC∽△ACD∽△CED,
∴AC2=AE•AD,CD2=DE•AD,
∴AE:ED=AC2:CD2=27:1
∴AF=27x,
∵AF-BF=16,
∴27x-3x=24x=16,
∴x=
 ,
,∴AB=AF+BF=3x+27x=30x=30×
 =20.
=20.点评:本题考查了全等三角形的判定和性质以及直角三角形的性质,是基础知识要熟练掌握.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 如图,直角三角形ABC的周长为24,且AB:BC=5:3,则AC=( )
如图,直角三角形ABC的周长为24,且AB:BC=5:3,则AC=( )| A、6 | B、8 | C、10 | D、12 |
 (2012•海陵区二模)如图,直角三角形纸片ABC中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B与点C重合,折痕与AB、BC的交点分别为D、E.
(2012•海陵区二模)如图,直角三角形纸片ABC中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B与点C重合,折痕与AB、BC的交点分别为D、E. 如图,直角三角形纸片ABC中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B与点C重合,折痕与AB、BC的交点分别为D、E.则DE的长为
如图,直角三角形纸片ABC中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B与点C重合,折痕与AB、BC的交点分别为D、E.则DE的长为 如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为
如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为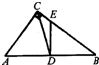 如图,直角三角形ABC中,∠ACB=90°,∠B=36°,D是AB的中点,ED⊥AB交BC于E,连接CD,则∠CDE:∠ECD=
如图,直角三角形ABC中,∠ACB=90°,∠B=36°,D是AB的中点,ED⊥AB交BC于E,连接CD,则∠CDE:∠ECD=