题目内容
10.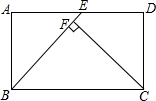 如图,矩形ABCD中,AB=2,BC=3,E是AD的中点,CF⊥BE于点F,则CF=2.4.
如图,矩形ABCD中,AB=2,BC=3,E是AD的中点,CF⊥BE于点F,则CF=2.4.
分析 根据相似三角形的判定与性质得出△ABE∽△FCB,得出$\frac{AB}{FC}$=$\frac{BE}{BC}$,进而得出答案.
解答 解:∵AD∥BC,
∴∠AEB=∠CBF,
∵∠A=90°,∠CFB=90°,
∴△ABE∽△FCB,
∴$\frac{AB}{FC}$=$\frac{BE}{BC}$,
∵AB=2,BC=3,E是AD的中点,
∴BE=2.5,
∴$\frac{2}{FC}$=$\frac{2.5}{3}$,
解得:FC=2.4.
故答案为:2.4.
点评 此题主要考查了相似三角形的判定与性质,根据已知得出△ABE∽△FCB是解题关键.

练习册系列答案
相关题目
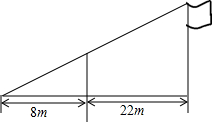 如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( ) 如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.