题目内容
1．对于任意的有理数a，b，定义新运算※：a※b=2ab+1，如（-3）※4=2×（-3）×4+1=-23．计算：3※（-5）=-29．分析 利用定义的新运算转化为有理数的混合运算，进一步计算得出答案即可．
解答 解：3※（-5）
=2×3×（-5）+1
=-30+1
=-29．
故答案为：-29．
点评 此题考查有理数的混合运算，理解定义运算的方法是解决问题的关键．
练习册系列答案
相关题目
11．下列各式中，不能用平方差公式分解因式的是（ ）
| A． | x4-y4 | B． | 4m2+n2 | C． | $\frac{1}{144}$-x4 | D． | （a+b）2-81 |
12．定义：如果10b=n，那么称b为n的劳格数，记为b=d（n）．
（1）根据劳格数的定义，可知：d（10）=1，d（102）=2，那么：d（103）=3．
（2）劳格数有如下运算性质：若m、n为正数，则d（mn）=d（m）+d（n）；d（$\frac{m}{n}$）=d（m）-d（n）．
根据运算性质，填空：$\frac{{d（{2^5}）}}{d（2）}$=5，若d（3）=0.477，则d（9）=0.954，d（0.3）=-0.523．
（3）下表中与x数对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数并改正．
（1）根据劳格数的定义，可知：d（10）=1，d（102）=2，那么：d（103）=3．
（2）劳格数有如下运算性质：若m、n为正数，则d（mn）=d（m）+d（n）；d（$\frac{m}{n}$）=d（m）-d（n）．
根据运算性质，填空：$\frac{{d（{2^5}）}}{d（2）}$=5，若d（3）=0.477，则d（9）=0.954，d（0.3）=-0.523．
（3）下表中与x数对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数并改正．
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d（x） | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
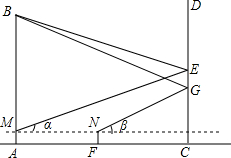如图，AB，CD表示两栋建筑，小明想利用建筑CD玻璃幕墙的反射作用来测建筑AB的高度，首先他在建筑AB的底部A处用测角仪测得其顶部B在建筑CD玻璃幕墙上的反射点E的仰角为α，然后他沿AC前进了10米到达点F处，再用测角仪测得建筑AB的顶部B在建筑CD玻璃幕墙上的反射点G的仰角为β，已知tanα=$\frac{1}{3}$，sinβ=$\frac{1}{3}$，测角仪置于水平高度1.5米的M、N处．试求建筑AB的高度．
如图，△ABC的三个点分别是A（1，2），B（3，3），C（2，6）