题目内容
6. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方程、抛物线的对称轴以及当x=0时的y值,即可得出a、b、c的正负,进而即可得出①错误;由x=-1时,y<0,即可得出a-b+c<0,进而即可得出②错误;由抛物线的对称轴为x=1结合x=0时y>0,即可得出当x=2时y>0,进而得出4a+2b+c=c>0,③成立;由二次函数图象与x轴交于不同的两点,结合根的判别式即可得出△=b2-4ac>0,④成立.综上即可得出结论.
解答 解:①∵抛物线开口向下,
∴a<0.
∵抛物线的对称轴为x=-$\frac{b}{2a}$=1,
∴b=-2a>0.
当x=0时,y=c>0,
∴abc<0,①错误;
②当x=-1时,y<0,
∴a-b+c<0,
∴b>a+c,②错误;
③∵抛物线的对称轴为x=1,
∴当x=2时与x=0时,y值相等,
∵当x=0时,y=c>0,
∴4a+2b+c=c>0,③正确;
④∵抛物线与x轴有两个不相同的交点,
∴一元二次方程ax2+bx+c=0,
∴△=b2-4ac>0,④正确.
综上可知:成立的结论有2个.
故选B.
点评 本题考查了二次函数图象与系数的关系、根的判别式以及二次函数图象上点的坐标特征,根据给定二次函数的图象逐一分析四条结论的正误是解题的关键.

练习册系列答案
相关题目
17. 为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有200名;
(2)表中x,y和m所表示的数分别为:x=100,y=30,m=5%;
(3)请补全条形统计图;
(4)若将抽取的若干名学生的实验成绩绘制成扇形统计图,则实验成绩为D类的扇形所对应的圆心角的度数是多少.
 为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有200名;
(2)表中x,y和m所表示的数分别为:x=100,y=30,m=5%;
(3)请补全条形统计图;
| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 百分比 | 30% | 50% | 15% | m |
 如图.∠A=90°,⊙O是△ABC的内切圆,内切圆半径为1,与三边的切点分别是点E,F,D,AC=4,求AB,BC的长.
如图.∠A=90°,⊙O是△ABC的内切圆,内切圆半径为1,与三边的切点分别是点E,F,D,AC=4,求AB,BC的长.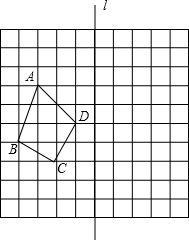 如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上. 如图,∠BAC=30°,P是∠BAC平分线上一点,PM∥AC交AB于M,PD⊥AC于D,若PD=10,则AM=20.
如图,∠BAC=30°,P是∠BAC平分线上一点,PM∥AC交AB于M,PD⊥AC于D,若PD=10,则AM=20. 如图,已知点C是线段AB的黄金分割点,若AB=2cm,则AC=$\sqrt{5}$-1cm.
如图,已知点C是线段AB的黄金分割点,若AB=2cm,则AC=$\sqrt{5}$-1cm.