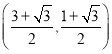题目内容
【题目】如图,![]() 是
是![]() 的中线,
的中线, ![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合).
重合).![]() 交射线
交射线![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
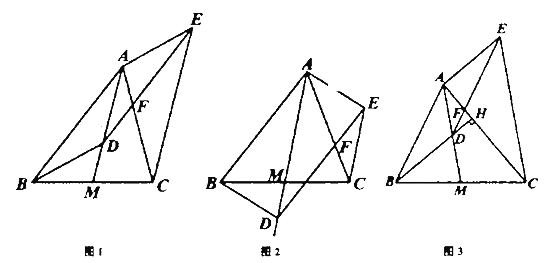
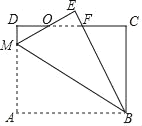
(1)如图1,当点![]() 在
在![]() 上时,求证:四边形
上时,求证:四边形![]() 是平行四边形;
是平行四边形;
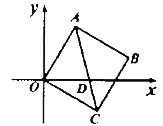
(2)如图2,当点![]() 在
在![]() 上运动时,(1)中的结论还成立吗?请直按写出你的结论;
上运动时,(1)中的结论还成立吗?请直按写出你的结论;
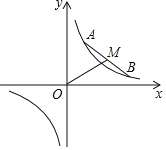
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() ,请求出
,请求出![]() 的度数.
的度数.
【答案】(1)见解析;(2)成立;(3)![]() .
.
【解析】
(1)0根据平行线的性质可得四边形![]() 是平行四边形,则
是平行四边形,则![]() ,根据三角形中线的性质,全等三角形的判断和平行四边形的判定即可得到答案;
,根据三角形中线的性质,全等三角形的判断和平行四边形的判定即可得到答案;
(2)由(1)的证明过程可知,点![]() 在
在![]() 上任意位置,都有四边形
上任意位置,都有四边形![]() 是平行四边形;
是平行四边形;
(3)取线段![]() 的中点
的中点![]() ,连接
,连接![]() .根据三角形中位线定理和直角三角函数即可解答.
.根据三角形中位线定理和直角三角函数即可解答.
解:⑴证明:过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]()
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中线,∴
的中线,∴![]() ,
,
∴![]() ≌
≌![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 是平行四边形..Com]
是平行四边形..Com]
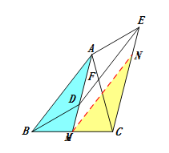
⑵结论:成立.
理由:由(1)的证明过程可知,点![]() 在
在![]() 上任意位置,都有四边形
上任意位置,都有四边形![]() 是平行四边形;
是平行四边形;
⑶如图,取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
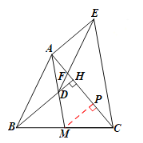
∵![]() ,∴
,∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,
,
![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目