题目内容
18.某中学公司组织初三505名学生外出社会综合实践活动,现打算租用A、B 两种型号的汽车,并且每辆车上都安排1名导游,如果租用这两种型号的汽车各5辆,则刚好坐满;如果全部租用B型汽车,则需13辆汽车,且其中一辆会有2个空位,其余汽车都坐满.(注:同种型号的汽车乘客座位数相同)(1)A、B两种型号的汽车分别有多少个乘客座位?
(2)综合考虑多种因素,最后该公司决定租用9辆汽车,问最多安排几辆B型汽车?
分析 (1)设A型汽车有x个乘客座位,B型汽车有y个乘客座位,根据各车的座位数和人数列出方程,求出x,y的值,即可得出答案;
(2)设安排B型汽车m辆,根据租用9辆汽车和总人数列出不等式,求出m的值即可得出答案.
解答 解:(1)设A型汽车有x个乘客座位,B型汽车有y个乘客座位,由题意得
$\left\{{\begin{array}{l}{5x+5y=505+10}\\{13y=505+13+2}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{x=63}\\{y=40}\end{array}}\right.$.
答:A型汽车有63个乘客座位,B型汽车有40个乘客座位;
(2)设安排B型汽车m辆,由题意得:
40m+63(m-9)≥505+9,
解得:m≤2$\frac{7}{23}$,
又∵m为整数,
∴m的最大值为2.
答:A型汽车有63个乘客座位,B型汽车有40个乘客座位,最多安排2辆B型汽车.
点评 此题考查了二元一次方程组和一元一次不等式的应用,读懂题意,找到关键描述语,找到所求的量的等量关系是解决问题的关键.

练习册系列答案
相关题目
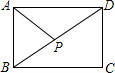 如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )
如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )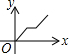
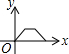
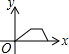
 如图所示,△ABC≌△CDA,AB=5,AC=7,BC=8,则AD的长是8.
如图所示,△ABC≌△CDA,AB=5,AC=7,BC=8,则AD的长是8. 如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG.
如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG. 如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5,求BC的长.
如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5,求BC的长. 如图,已知直线a,b,c相交于点O,且a⊥c,垂足为O,若∠1=50°,则∠2的度数为140°.
如图,已知直线a,b,c相交于点O,且a⊥c,垂足为O,若∠1=50°,则∠2的度数为140°.