题目内容
6.阅读材料:求l+2+22+23+24+…+22013的值.
解:设S=l+2+22+23+24+…+22012+22013,将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014.
将下式减去上式,得2S-S=22014一l
即S=22014一l,
即1+2+22+23+24+…+22013=22014一l
仿照此法计算:
(1)1+3+32+33+…+3100
(2)1+$\frac{1}{2}+\frac{1}{2^2}\frac{1}{2^3}$+…+$\frac{1}{{{2^{100}}}}$.
分析 (1)设S=1+3+32+33+…+3100,两边乘以3得出3S=3+32+33+34+35+…+3100+3101,将下式减去上式即可得出答案;
(2)设S=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$,两边乘以$\frac{1}{2}$得出$\frac{1}{2}$S=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{101}}$,将下式减去上式即可得出答案.
解答 解:(1)设S=1+3+32+33+…+3100,
两边乘以3得:3S=3+32+33+34+35+…+3100+3101,
将下式减去上式,得3S-S=3101-l
即S=$\frac{{3}^{101}-1}{2}$,
即1+3+32+33+34+…+3100=$\frac{{3}^{101}-1}{2}$
(2)设S=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$,
两边乘以$\frac{1}{2}$得:$\frac{1}{2}$S=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{101}}$,
将下式减去上式得:-$\frac{1}{2}$S=$\frac{1}{{2}^{101}}$-1,
解得:S=2-$\frac{1}{{2}^{100}}$,
即1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$=2-$\frac{1}{{2}^{100}}$.
点评 本题考查了有理数的混合运算的应用,能读懂题意是解此题的关键,主要培养学生的理解能力.

 如图,三角形ABC经过平移得到三角形DEF,则图中平行的线段共有( )
如图,三角形ABC经过平移得到三角形DEF,则图中平行的线段共有( )| A. | 0组 | B. | 3组 | C. | 6组 | D. | 9组 |
| A. | (a+b)2=a2+b2 | B. | (x+6)(x-6)=x2-6 | C. | (x+2)2=x2+2x+4 | D. | (x-y)2=(y-x)2 |
| A. | m8 | B. | m16 | C. | m0 | D. | 2m4 |
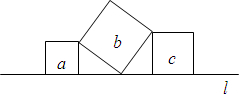 如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和6,则c的面积为1.
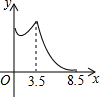
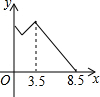
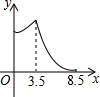
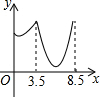
如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和6,则c的面积为1.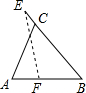 如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )
如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )