题目内容
13. 如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG.
如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG.(1)说明:DC∥AB;
(2)求∠PFH的度数.
分析 (1)由DC∥FP知∠3=∠2=∠1,可得;
(2)由(1)利用平行线的判定得到AB∥PF∥CD,根据平行线的性质得到∠AGF=∠GFP,∠DEF=∠EFP,然后利用已知条件即可求出∠PFH的度数.
解答 解:(1)∵DC∥FP,
∴∠3=∠2,
又∵∠1=∠2,
∴∠3=∠1,
∴DC∥AB;
(2)∵DC∥FP,DC∥AB,∠DEF=28°,
∴∠DEF=∠EFP=28°,AB∥FP,
又∵∠AGF=80°,
∴∠AGF=∠GFP=80°,
∴∠GFE=∠GFP+∠EFP=80°+28°=108°,
又∵FH平分∠EFG,
∴∠GFH=$\frac{1}{2}$∠GFE=54°,
∴∠PFH=∠GFP-∠GFH=80°-54°=26°.
点评 此题主要考查了平行线的性质与判定,首先利用同位角相等两直线平行证明直线平行,然后利用平行线的性质得到角的关系解决问题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
2.在整式5abc,-7x2+1,-$\frac{2x}{5}$,3.14,$\frac{4x-y}{2}$中,单项式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
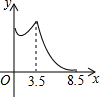
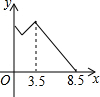
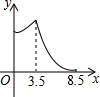
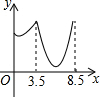
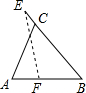 如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )
如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )