题目内容
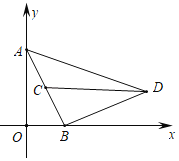
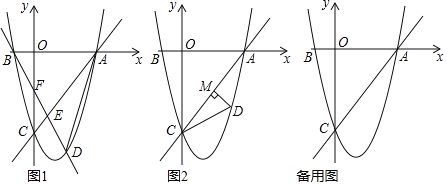
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a≠0)经过点A(6,﹣3),对称轴是直线x=4,顶点为B,OA与其对称轴交于点M,M、N关于点B对称.
(1)求这条抛物线的表达式和点B的坐标;
(2)联结ON、AN,求△OAN的面积;
(3)点Q在x轴上,且在直线x=4右侧,当∠ANQ=45°时,求点Q的坐标.
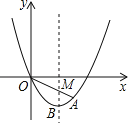
【答案】(1)y=![]() x2﹣2x,点B的坐标(4,﹣4);(2)S△OAN=12;(3)点Q的坐标(34,0).
x2﹣2x,点B的坐标(4,﹣4);(2)S△OAN=12;(3)点Q的坐标(34,0).
【解析】
(1)根据直线x=4和A(6,﹣3)列出方程组,求出a、b即可求出解析式,然后将x=4代入函数解析式,求得得y=﹣4,所以点B的坐标(4,﹣4);
(2)连结ON、AN,先求出M(4,﹣2),由M、N关于点B对称,求出N(4,﹣6),于是MN=4,所以S△OAN=![]() MN|xA|=
MN|xA|=![]() ×4×6=12;
×4×6=12;
(3)设对称轴直线x=4与x轴交于点T,抛物线与x轴另一个交点为P,则P(8,0),直线AN与x轴交于点P,连接NQ,连接NA、AP,过点P作PR⊥PN,与NQ交于点R,过R作RH⊥x轴于点H.由∠PNR=∠ANQ=45°,则∠PRN=45°=∠PNR,所以PR=PN,易证△PTN≌△RHP(AAS),则RH=PT=4,PH=TN=6,TH=10,由HR∥TN,列出比例式求出HQ=20,于是OQ=OP+PH+HQ=8+6+20=34,所以点Q的坐标(34,0).
(1)由题意可得
 ,
,
解得a=![]() ,b=﹣2,
,b=﹣2,
∴抛物线的表达式y=![]() x2﹣2x
x2﹣2x
将x=4代入,得y=﹣4,
∴点B的坐标(4,﹣4);
(2)连结ON、AN,如图1.

∵A(6,﹣3),
∴直线OA:y=﹣![]() x,
x,
将x=4代入,y=﹣2,
∴M(4,﹣2),
∵M、N关于点B对称,B(4,﹣4),
∴N(4,﹣6),
∴MN=4,
∴S△OAN=![]() MN|xA|=
MN|xA|=![]() ×4×6=12;
×4×6=12;
(3)设对称轴直线x=4与x轴于点T,抛物线与x轴另一个交点为P,则P(8,0).
∵A(6,﹣3),N(4,﹣6),
∴直线AN:y=![]() ,
,
令y=0,则x=8,
∴直线AN与x轴交点(8,0),
即直线AN与x轴交于点P,
如图2,连接NQ,连接NA、AP,过点P作PR⊥PN,与NQ交于点R,过R作RH⊥x轴于点H.

∵∠PNR=∠ANQ=45°,
∴∠PRN=45°=∠PNR,
∴PR=PN,
易证△PTN≌△RHP(AAS),
∴RH=PT=4,PH=TN=6,
∴TH=10,
![]()
![]() ∴HQ=20,
∴HQ=20,
∴OQ=OP+PH+HQ=8+6+20=34,
点Q的坐标(34,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案