题目内容
已知函数y=ax2+bx+c,当y>0时,﹣
 <x<
<x<
 .则函数y=cx2﹣bx+a的图象可能是图中的( )
.则函数y=cx2﹣bx+a的图象可能是图中的( )
A.
 B.
B.

C.
 D.
D.

B【考点】二次函数的图象.
【分析】当y>0时,﹣
 <x<
<x<
 ,所以可判断a<0,函数y=ax2+bx+c与x轴的交点为(﹣
,所以可判断a<0,函数y=ax2+bx+c与x轴的交点为(﹣
 ,0)和(
,0)和(
 ,0),即可求得﹣
,0),即可求得﹣
 =﹣
=﹣
 ,
,
 =﹣
=﹣
 ,得出a=6b,a=﹣6c,则b=﹣c,不妨设c=1,进而得出解析式,找出符合要求的答案.
,得出a=6b,a=﹣6c,则b=﹣c,不妨设c=1,进而得出解析式,找出符合要求的答案.
【解答】解:∵函数y=ax2+bx+c,当y>0时,﹣
 <x<
<x<
 .
.
∴a<0,c>0,函数y=ax2+bx+c与x轴的交点为(﹣
 ,0)和(
,0)和(
 ,0),
,0),
∴﹣
 =﹣
=﹣
 +
+
 =﹣
=﹣
 ,
,
 =﹣
=﹣
 ×
×
 =﹣
=﹣
 ,
,
∴a=6b,a=﹣6c,
∴b=﹣c,不妨设c=1
∴函数y=cx2﹣bx+a为函数y=x2+x﹣6
即y=(x﹣2)(x+3)
∴与x轴的交点坐标是(2,0),(﹣3,0).
故选B.
【点评】本题考查了二次函数的图象,根与系数的关系,根据二次函数与不等式的关系判断出a、b、c的正负情况以及a、c的关系是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 .
.
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.

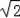
 ≈1.414,
≈1.414,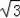
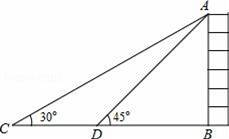






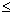 3时,y= ;
3时,y= ; .
. (3)就0<t
(3)就0<t