Question

17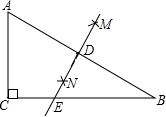．如图，Rt△ABC中，∠ACB=90°，分别以点A、点B为圆心，大于$\frac{1}{2}$AB的长为半径作弧，两弧交于点M、N，直线MN交BC于点D，若AC=2，BC=3，则CD的长为$\frac{\sqrt{13}}{2}$．

Answer 1

分析 利用基本作法得到MN垂直平分AB，则AD=BD，再利用勾股定理计算出AB，然后根据直角三角形斜边上的中线确定CD的长．

解答 解：由作法得MN垂平分AB，
所以AD=BD，
因为AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$，
所以CD=$\frac{1}{2}$AB=$\frac{\sqrt{13}}{2}$．
故答案为$\frac{\sqrt{13}}{2}$．

点评 本题考查了作图-基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．