题目内容
9.已知正方形ABCD,点E在线段BC上,且BE=2CE,连接AE,将△ABE沿AE翻折,点B落在点B1处,则tan∠DAB1的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{12}$ |
分析 如图,设直线AB1与DC相交于点M,AE的延长线交DC的延长线于F,根据相似三角形的性质得到$\frac{AB}{CF}=\frac{BE}{CE}$=2,设正方形的边长=2a,则CF=a,根据已知条件得到AM=MF,设DM=x,则CM=2a-x.又CF=a,求得AM=MF=3a-x,根据勾股定理得到DM=$\frac{5a}{6}$,于是得到结论.
解答  解:如图,设直线AB1与DC相交于点M,AE的延长线交DC的延长线于F,
解:如图,设直线AB1与DC相交于点M,AE的延长线交DC的延长线于F,
∴△ABE∽△CEF,
∴$\frac{AB}{CF}=\frac{BE}{CE}$=2,
设正方形的边长=2a,
则CF=a,
由题意翻折得:∠1=∠2,
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF,
设DM=x,则CM=2a-x.
又CF=a,
∴AM=MF=3a-x,
在Rt△ADM中,AD2+DM2=AM2,
∴(2a)2+x2=(3a-x)2,
∴x=$\frac{5a}{6}$,
∴DM=$\frac{5a}{6}$,
∴tan∠DAB1═$\frac{DM}{AD}$=$\frac{\frac{5a}{6}}{2a}$=$\frac{5}{12}$;
故选D.
点评 本题考查了翻折变换(折叠问题)正方形的性质,等腰三角形的判定和性质,解直角三角形,正确的作出图形是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
20.下面四个实数中,是无理数的为( )
| A. | 0 | B. | $\sqrt{3}$ | C. | -2 | D. | $\frac{1}{7}$ |
 如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,∠B=∠EDC,DF∥AC,试说明:∠FDE=∠A.
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,∠B=∠EDC,DF∥AC,试说明:∠FDE=∠A.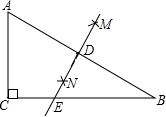 如图,Rt△ABC中,∠ACB=90°,分别以点A、点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧交于点M、N,直线MN交BC于点D,若AC=2,BC=3,则CD的长为$\frac{\sqrt{13}}{2}$.
如图,Rt△ABC中,∠ACB=90°,分别以点A、点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧交于点M、N,直线MN交BC于点D,若AC=2,BC=3,则CD的长为$\frac{\sqrt{13}}{2}$.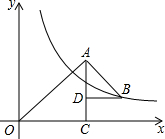 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为9.
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为9.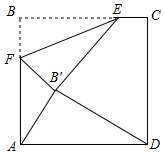 如图,正方形ABCD的边长为8,E为BC上一定点,BE=6,F为AB上一动点,把△BEF沿EF折叠,点B落在点B'处,当△AFB'恰好为直角三角形,B'D的长为$\frac{4}{5}\sqrt{65}$或2$\sqrt{2}$.
如图,正方形ABCD的边长为8,E为BC上一定点,BE=6,F为AB上一动点,把△BEF沿EF折叠,点B落在点B'处,当△AFB'恰好为直角三角形,B'D的长为$\frac{4}{5}\sqrt{65}$或2$\sqrt{2}$. 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.