题目内容
7.我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45°,那么该等腰三角形的顶角等于90°或30°.分析 根据新定理,设最小角为x,则最大角为x+45°,再分类讨论求出顶角的度数.
解答 解:设最小角为x,则最大角为x+45°,
当最小角是顶角时,则x+x+45°+x+45°=180°,
解得x=30°,
当最大角为顶角时,x+x+45°+x=180°,
解得x=45°,
即等腰三角形的顶角为30°或90°,
故答案为90°或30°.
点评 本题主要考查了等腰三角形的性质,解题的关键是理解新定义以及分类讨论解题思想,此题难度一般.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
16.在平面直角坐标系中,将点P(-2,1)向右平移3个单位长度,再向下平移4个单位长度得到点P′的坐标是( )
| A. | (2,4) | B. | (1,-3) | C. | (1,5) | D. | (-5,5) |
 如图,在△ABC中,∠ACB=90°,AC=8,AB=10,ED垂直平分AC交AB于点E,则ED的长为3.
如图,在△ABC中,∠ACB=90°,AC=8,AB=10,ED垂直平分AC交AB于点E,则ED的长为3. 如图,?ABCD的对角线BD上有两点E、F,请你添加一个条件,使四边形AECF是平行四边形,你添加的条件是BE=DF(答案不唯一).
如图,?ABCD的对角线BD上有两点E、F,请你添加一个条件,使四边形AECF是平行四边形,你添加的条件是BE=DF(答案不唯一).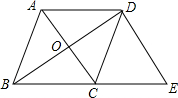 如图,在平行四边形ABCD中,对角线AC、BD交于点O,DE∥AC交BC的延长线于点E.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,DE∥AC交BC的延长线于点E.