题目内容
17.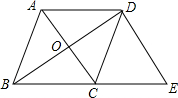 如图,在平行四边形ABCD中,对角线AC、BD交于点O,DE∥AC交BC的延长线于点E.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,DE∥AC交BC的延长线于点E.(1)求证:△ABC≌△DCE;
(2)若CD=CE,求证:AC⊥BD.
分析 (1)由平行四边形的性质得出AB=CD,AB∥CD,由平行线证出∠ABC=∠DCE,∠BAC=∠ACD,∠ACB=∠DEC,由AAS证明△ABC≌△DCE即可;
(2)由(1)得:△ABC≌△DCE,得出AC=DE,证出四边形ACED是平行四边形,得出AD=CE,证出AD=CD,因此四边形ABCD是菱形,即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABC=∠DCE,∠BAC=∠ACD,
∵DE∥AC,
∴∠ACB=∠DEC,
在△ABC和△DCE中,$\left\{\begin{array}{l}{∠ABC=∠DCE}&{\;}\\{∠ACB=∠DEC}&{\;}\\{AB=DC}&{\;}\end{array}\right.$,
∴△ABC≌△DCE(AAS);
(2)证明:由(1)得:△ABC≌△DCE;
∴AC=DE,
∵AC∥DE,
∴四边形ACED是平行四边形,
∴AD=CE,
∵CD=CE,
∴AD=CD,
∴四边形ABCD是菱形,
∴AC⊥BD.
点评 本题考查的是菱形的性质、全等三角形的判定与性质及平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
8. 如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
 如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )| A. | 105° | B. | 115° | C. | 125° | D. | 75° |
 如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017).
如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017). 如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )
如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )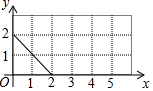 如图,动点P从(0,2)出发,沿所示的方向在矩形网格中运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,若第一次碰到矩形的边时坐标为P1(2,0),则P2017的坐标为(2,0).
如图,动点P从(0,2)出发,沿所示的方向在矩形网格中运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,若第一次碰到矩形的边时坐标为P1(2,0),则P2017的坐标为(2,0).