题目内容
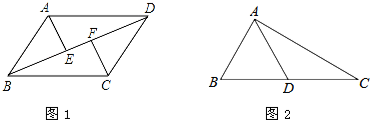
如图(1),在Rt△ABC, ∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M。
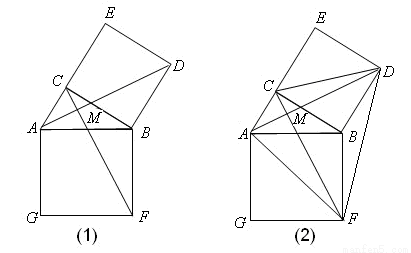
(1)求证:△ABD≌△FBC;
(2)如图(2),已知AD=6,求四边形AFDC的面积;
(3)在△ABC中,设BC=a,AC=b,AB=c,当∠ACB≠90°时,c2≠a2 +b2。在任意△ABC中,c2=a2 +b2+k。就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可)。
【答案】
解:(1)证明:∵正方形ABFG、BCED,∴AB=FB,CB=DB,∠ABF=∠CBD=90°,
∴∠ABF+∠ABC=∠CBD+∠ABC,即∠ABD=∠CBF。
在△ABD与△FBC中,∵AB=FB,∠ABD=∠CBF,DB= CB,
∴△ABD≌△FBC(SAS)。
(2)由(1)△ABD≌△FBC得,AD=FC,∠BAD=∠BFC。
∴∠AMF=180°-∠BAD-∠CMA=180°-∠BFC-∠BMF=180°-90°=90°。∴AD⊥CF。
∵AD=6,∴FC= AD=6。
∴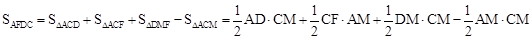
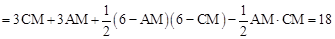 。
。
(3)-12<k<12。
【解析】
试题分析:(1)根据正方形的性质易由SAS证明△ABD≌△FBC。
(2)由(1)△ABD≌△FBC证得AD=FC,∠BAD=∠BFC,进一步由三角形内角和定理证得AD⊥CF,从而根据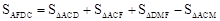 求出答案。
求出答案。
(3)由a=3,b=2,c2=a2
+b2+k得c2=13+k,即 ,根据三角形三边关系,得
,根据三角形三边关系,得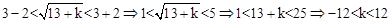 。
。

练习册系列答案
相关题目
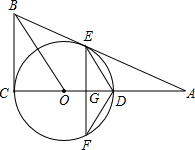 (2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
(2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
 如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.
如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D. 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.