题目内容
【题目】如图![]() ,
,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 是
是![]() 与
与![]() 的交点,且
的交点,且![]() .
.

![]() 图
图![]() 中是否存在与
中是否存在与![]() 相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
![]() 求证:
求证:![]() ;
;
![]() 若将“点
若将“点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上”和“点
上”和“点![]() 是
是![]() 与
与![]() 的交点,且
的交点,且![]() ”分别改为“点
”分别改为“点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上”和“点
的延长线上”和“点![]() 是
是![]() 的延长线与
的延长线与![]() 的交点,且
的交点,且![]() ”,其他条件不变(如图
”,其他条件不变(如图![]() ).当
).当![]() ,
,![]() 时,求
时,求![]() 的长(用含
的长(用含![]() 、
、![]() 的式子表示).
的式子表示).
【答案】![]() .
.![]() 证明见解析
证明见解析![]()
![]() 的长为
的长为![]() .
.
【解析】
(1)运用等腰三角形的性质及三角形的外角性质就可解决问题.
(2)过点E作EG∥AC,交AB于点G,如图1,要证BE=CE,只需证BG=AG,由DF=FE可证到DA=AG,只需证到DA=BG即DG=AB,也即DG=AC即可.只需证明△DCA≌△△EDG即可解决问题.
(3)过点A作AH⊥BC,垂足为H,如图2,可求出BC=2cosα.过点E作EG∥AC,交AB的延长线于点G,易证△DCA≌△△EDG,则有DA=EG,CA=DG=1.易证△ADF∽△GDE,则有![]() .由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=
.由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=![]() ,即GE=
,即GE=![]() .易证△ABC∽△GBE,则有
.易证△ABC∽△GBE,则有![]() ,从而可以求出BE.
,从而可以求出BE.
![]() .
.
证明:∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.![]() 过点
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图
,如图![]() ,
,
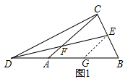
则有![]() .
.
在![]() 和
和![]() 中,
中,
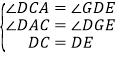
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.![]() 过点
过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,如图
,如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
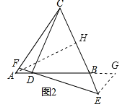
在![]() 和
和![]() 中,
中,
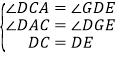
∴![]() .
.
∴![]() ,
,![]()
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图
,如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 的长为
的长为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】(1) 观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| 0.01 | x | 1 | y | 100 |
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知![]() ≈1.414,则
≈1.414,则![]() =________,
=________,![]() =_______;
=_______;
②![]() = 0.274,记
= 0.274,记![]() 的整数部分为x,则
的整数部分为x,则![]() =___________.
=___________.






