题目内容
 已知双曲线y=
已知双曲线y=| 4 |
| x |
| 1 |
| 4 |
| AE2+BF2 |
| EF2 |
考点:反比例函数综合题,反比例函数与一次函数的交点问题,勾股定理,相似三角形的判定与性质
专题:计算题,压轴题
分析:方法1:由所求的式子联想到勾股定理,故过A作AG⊥y轴于G,过B作BH⊥x轴于H,设FH=a,则有OF=4+a,BF2=a2+1.易证△AEG∽△BFH,从而有
=
=
=4,就可用a的代数式表示AE2、EF2,然后代入所求的式子就可解决问题;
方法2:过点A作AG∥BF,交x轴于点G,连接EG,易证△AOG≌△BOF,则有AG=BF,OG=OF.根据线段的垂直平分线的性质可得EG=EF,在Rt△GAE中运用勾股定理可得AG2+AE2=GE2,然后通过等量代换就可解决问题.
| AE |
| BF |
| EG |
| FH |
| AG |
| BH |
方法2:过点A作AG∥BF,交x轴于点G,连接EG,易证△AOG≌△BOF,则有AG=BF,OG=OF.根据线段的垂直平分线的性质可得EG=EF,在Rt△GAE中运用勾股定理可得AG2+AE2=GE2,然后通过等量代换就可解决问题.
解答:解1:过A作AG⊥y轴于G,过B作BH⊥x轴于H,设直线AC与x轴交于点K,如图,

联立
,
解得:
,
.
∵点A在点B的左侧,
∴A(-4,-1),B(4,1).
∴AG=4,OG=1,OH=4,BH=1.
设FH=a,则有OF=OH+FH=4+a,BF2=FH2+BH2=a2+1.
∵AC⊥CF,OE⊥OK,
∴∠CFK=90°-∠CKF=∠OEK.
∵AG⊥y轴,BH⊥x轴,
∴∠AGE=∠BHF=90°.
∴△AEG∽△BFH.
∴
=
=
=4.
∴AE2=16BF2=16(a2+1),EG=4FH=4a.
∴OE=
=|4a-1|.
∴EF2=(4a-1)2+(4+a)2=17(a2+1).
∴
=
=1.
故答案为:1.
解2:过点A作AG∥BF,交x轴于点G,连接EG,如图.

则有∠GAC=∠FCA=90°,∠AGO=∠BFO.
∵双曲线y=
与直线y=
x都关于点O成中心对称,
∴它们的交点也关于点O成中心对称,即OA=OB.
在△AOG和△BOF中,
,
∴△AOG≌△BOF,
∴AG=BF,OG=OF.
∵OE⊥GF,
∴EG=EF.
∵∠GAC=90°,
∴AG2+AE2=GE2,
∴BF2+AE2=EF2,
∴
=1.
故答案为:1.

联立
|
解得:
|
|
∵点A在点B的左侧,
∴A(-4,-1),B(4,1).
∴AG=4,OG=1,OH=4,BH=1.
设FH=a,则有OF=OH+FH=4+a,BF2=FH2+BH2=a2+1.
∵AC⊥CF,OE⊥OK,
∴∠CFK=90°-∠CKF=∠OEK.
∵AG⊥y轴,BH⊥x轴,
∴∠AGE=∠BHF=90°.
∴△AEG∽△BFH.
∴
| AE |
| BF |
| EG |
| FH |
| AG |
| BH |
∴AE2=16BF2=16(a2+1),EG=4FH=4a.
∴OE=
|
∴EF2=(4a-1)2+(4+a)2=17(a2+1).
∴
| AE2+BF2 |
| EF2 |
| 16(a2+1)+(a2+1) |
| 17(a2+1) |
故答案为:1.
解2:过点A作AG∥BF,交x轴于点G,连接EG,如图.

则有∠GAC=∠FCA=90°,∠AGO=∠BFO.
∵双曲线y=
| 4 |
| x |
| 1 |
| 4 |
∴它们的交点也关于点O成中心对称,即OA=OB.
在△AOG和△BOF中,
|
∴△AOG≌△BOF,
∴AG=BF,OG=OF.
∵OE⊥GF,
∴EG=EF.
∵∠GAC=90°,
∴AG2+AE2=GE2,
∴BF2+AE2=EF2,
∴
| AE2+BF2 |
| EF2 |
故答案为:1.
点评:本题考查了反比例函数与一次函数交点问题、相似三角形的判定与性质、勾股定理、全等三角形的判定与性质、线段的垂直平分线的性质等知识,而由线段的平方联想到勾股定理是解决本题的关键.

练习册系列答案
相关题目
计算(-
)-1的倒数为( )
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
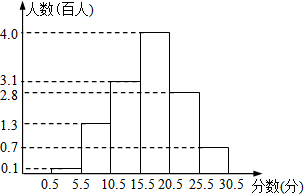 2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答:
2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答: