题目内容
已知,在△ABC中,点E在AB上,AE:EB=1:2,EF∥BC,交AC于点F,AD∥BC,交CE延长线于点D,设△AEF的面积为3.求△CEF和△ADE的面积.
考点:相似三角形的判定与性质
专题:
分析:由平行可得
=
,则可得
=
,代入可求得△CEF的面积,又可得△CEF∽△CDA,借助相似比可求得△CDA的面积,可进一步求得△ADE的面积.
| AF |
| FC |
| AE |
| BE |
| S△AEF |
| S△CEF |
| AF |
| FC |
解答:解:
∵EF∥BC,
∴
=
=
,
∴
=
,即
=
,
∴S△CEF=6,
∵AD∥BC,
∴EF∥AD,
∴△CEF∽△CDA,
∵AE:EB=1:2,
∴AF:FC=1:2,
∴CF:AC=2:3,
∴
=(
)2=(
)2=
,
即
=
,解得S△CDA=13.5,
∴S△ADE=S△CAD-S△CEF-S△AEF=13.5-6-3=4.5.
∵EF∥BC,
∴
| AF |
| FC |
| AE |
| EB |
| 1 |
| 2 |
∴
| S△AEF |
| S△CEF |
| 1 |
| 2 |
| 3 |
| S△CEF |
| 1 |
| 2 |
∴S△CEF=6,
∵AD∥BC,
∴EF∥AD,
∴△CEF∽△CDA,
∵AE:EB=1:2,
∴AF:FC=1:2,
∴CF:AC=2:3,
∴
| S△CEF |
| S△CDA |
| CF |
| CA |
| 2 |
| 3 |
| 4 |
| 9 |
即
| 6 |
| S△CDA |
| 4 |
| 9 |
∴S△ADE=S△CAD-S△CEF-S△AEF=13.5-6-3=4.5.
点评:本题主要考查相似三角形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键,注意等高三角形的面积比等于底的比.

练习册系列答案
相关题目
已知AB是⊙O的切线,在下列给出的条件中,能判断出AB⊥CD的是( )
| A、AB与⊙O相切于点C |
| B、CD是⊙O的直径 |
| C、AB与⊙O相切于点C,CD是直径 |
| D、CD是⊙O的弦 |
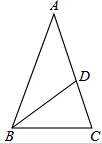 如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,若AC=3,则BD的长为( )
如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,若AC=3,则BD的长为( )A、
| ||||
B、-3
| ||||
C、
| ||||
D、
|
已知⊙O上有一点A,直线l经过点A,则l与⊙O的位置关系是( )
| A、相切 | B、相交 |
| C、相离 | D、相交或相切 |
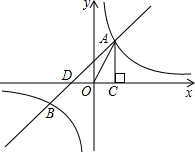 如图,已知反比例函数y1=
如图,已知反比例函数y1= 如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.
如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.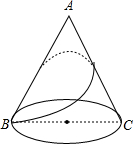 有一圆锥形粮堆如图所示,其母线长为12m,底面直径长为6m,一只小猫从B处绕粮堆巡视一圈后又回到B处,则它所行走最短路程是
有一圆锥形粮堆如图所示,其母线长为12m,底面直径长为6m,一只小猫从B处绕粮堆巡视一圈后又回到B处,则它所行走最短路程是