题目内容
9.因式分解:x2-8=(x+$2\sqrt{2}$)(x-$2\sqrt{2}$).分析 首先把8化成${(2\sqrt{2})}^{2}$,然后根据平方差公式,在实数范围内,把x2-8进行因式分解即可.
解答 解:x2-8
=x2-${(2\sqrt{2})}^{2}$
=(x+$2\sqrt{2}$)(x-$2\sqrt{2}$)
故答案为:(x+$2\sqrt{2}$)(x-$2\sqrt{2}$).
点评 此题主要考查了实数范围内分解因式问题的应用,解答此题的关键是要明确:实数范围内分解因式是指可以把因式分解到实数的范围(可用无理数的形式来表示),一些式子在有理数的范围内无法分解因式,可是在实数范围内就可以继续分解因式.

练习册系列答案
相关题目
20.一辆汽车在直路上行驶,两次拐弯后,仍按原来的方向行驶,那么这两次拐弯是( )
| A. | 第一次向右拐30°,第二次向右拐30° | |
| B. | 第一次向右拐30°,第二次向右拐150° | |
| C. | 第一次向左拐30°,第二次向右拐150° | |
| D. | 第一次向左拐30°,第二次向右拐30° |
17. 如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )
如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )
 如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )
如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )| A. | 72° | B. | 54° | C. | 45° | D. | 36° |
14.如果a>b,那么下列各式中正确的是( )
| A. | a-2<b-2 | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | -2a<-2b | D. | -a>-b |
1.已知直角三角形的周长为$4+\sqrt{26}$,斜边为4,则该三角形的面积是( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{4}$ |
18. 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
19.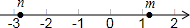 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
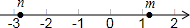 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-n>0 | B. | |n|-|m|<0 | C. | m+3<n+3 | D. | -m>-n |