题目内容
 如图,在△ABC中,D、E两点分别在边BC、AC上,AE:EC=CD:BD=1:2,AD与BE相交于点F,若△ABC的面积为21,则△ABF的面积为
如图,在△ABC中,D、E两点分别在边BC、AC上,AE:EC=CD:BD=1:2,AD与BE相交于点F,若△ABC的面积为21,则△ABF的面积为考点:相似三角形的判定与性质
专题:
分析:根据等高的两个三角形底边的关系,可得两个三角形面积的关系,根据相似三角形判定与性质,可得AE:EG=AF:FD=3:4,根据比例的性质,可得AF:AD=3:7,再根据等高的两个三角形底边的关系,可得两个三角形面积的关系.
解答:解:如图,过D作DG∥BE,角AC与G, ,
,
∵AE:EC=CD:BD=1:2,△ABC的面积为21,
∴S△ABE:S△BCE=S△ADC:S△ABD=1:2,
∴S△ABD=
S△ABC=
×21=14,
∵DG∥BE,
∴△CDG∽△CBE,△AEF∽△AGD,
∴
=
=
,
GE=
CE,AE=
CE,
AE:EG=AF:FD=3:4,
AF:AD=3:7.
S△ABF:S△ABD=3:7,
S△ABF=
=
×14=6,
故答案为:6.
 ,
,∵AE:EC=CD:BD=1:2,△ABC的面积为21,
∴S△ABE:S△BCE=S△ADC:S△ABD=1:2,
∴S△ABD=
| 2 |
| 3 |
| 2 |
| 3 |
∵DG∥BE,
∴△CDG∽△CBE,△AEF∽△AGD,
∴
| CG |
| GE |
| DC |
| BD |
| 1 |
| 2 |
GE=
| 2 |
| 3 |
| 1 |
| 2 |
AE:EG=AF:FD=3:4,
AF:AD=3:7.
S△ABF:S△ABD=3:7,
S△ABF=
| 3S△ABD |
| 7 |
| 3 |
| 7 |
故答案为:6.
点评:本题考查了相似三角形的判定与性质,利用了等高的两个三角形的面积与底边的关系,相似三角形的判定与性质,题目有点难度.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、同旁内角互补,两直线平行 |
| B、垂线段最短 |
| C、在同一平面内,过一点有且只有一条直线与已知直线垂直 |
| D、直线外一点到这条直线的垂线段叫做点到直线的距离 |
数轴上到表示-2的点距离为4的点所表示的数是( )
| A、1.5 | B、-6 |
| C、1或-6 | D、2或-6 |
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3 M2,对角线A1M2和A3B3交于点M3;…,依此类推,这样作的第4个正方形对角线交点的坐标为M4(
如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3 M2,对角线A1M2和A3B3交于点M3;…,依此类推,这样作的第4个正方形对角线交点的坐标为M4(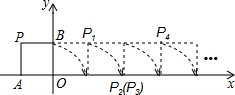 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2014次,点P依次落在点P1,P2,P3,…P2013,P2014的位置,记Pi(xi,yi),i=1,2,3,…,2013,2014,则P2014的坐标
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2014次,点P依次落在点P1,P2,P3,…P2013,P2014的位置,记Pi(xi,yi),i=1,2,3,…,2013,2014,则P2014的坐标