题目内容
 已知边长为2的等边△ABC中,点D为BC的中点,动点P在AC上,在△BPD的周长最小的情况下,AP的长度为
已知边长为2的等边△ABC中,点D为BC的中点,动点P在AC上,在△BPD的周长最小的情况下,AP的长度为考点:轴对称-最短路线问题,等边三角形的性质
专题:
分析:作点D关于AC的对称点D′,连接BD′与AC相交,根据轴对称确定最短路线问题,BD′与AC的交点即为所求的点P,连接CD′,求出AB∥CD′,判断出△ABP和△CD′P相似,根据相似三角形对应边成比例求出
,然后求解即可.
| AP |
| PC |
解答: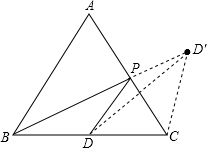 解:如图,作点D关于AC的对称点D′,连接BD′与AC相交,
解:如图,作点D关于AC的对称点D′,连接BD′与AC相交,
则BD′与AC的交点即为△BPD的周长最小时的点P,
连接CD′,由轴对称的性质得,∠PCD′=∠ACB=60°,CD′=CD=
BC=1,
∴∠BCD′=60°×2=120°,
∵∠ABC+∠BCD′=60°+120°=180°,
∴AB∥CD′,
∴△ABP∽△CD′P,
∴
=
=2,
∴AP=
×2=
.
故答案为:
.
 解:如图,作点D关于AC的对称点D′,连接BD′与AC相交,
解:如图,作点D关于AC的对称点D′,连接BD′与AC相交,则BD′与AC的交点即为△BPD的周长最小时的点P,
连接CD′,由轴对称的性质得,∠PCD′=∠ACB=60°,CD′=CD=
| 1 |
| 2 |
∴∠BCD′=60°×2=120°,
∵∠ABC+∠BCD′=60°+120°=180°,
∴AB∥CD′,
∴△ABP∽△CD′P,
∴
| AP |
| PC |
| AB |
| CD′ |
∴AP=
| 2 |
| 2+1 |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查了轴对称确定最短路线问题,等边三角形的性质,相似三角形的判定与性质,熟练掌握轴对称确定最短路线的方法找出点P的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 填写推理理由:
填写推理理由: 等腰△ABC中,BD为腰上的高.∠A=50°,则∠DBC的度数为
等腰△ABC中,BD为腰上的高.∠A=50°,则∠DBC的度数为