题目内容
(本小题满分10分)
(1)解方程: ;
;
(2)解不等式: ≤
≤ ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.

(1)x=-6;(2)x≥5.
【解析】
试题分析:(1)首先进行去分母,将其转化为整式方程,然后进行解一元一次方程,最后对所求的解进行验根;(2)首先进行去分母,然后进行解不等式,需要注意的就是在不等式的左右两边同时乘以或除以一个负数,不等符号需要改变.
试题解析:(1)去分母,得3x+6-2x=0 解得x=-6,
经检验,x=-6是原方程的解.
(2)去分母,得 6+2x-1≤3x, 解得x≥5
它的解集在数轴上可表示为:
考点:解分式方程、解不等式.
考点分析: 考点1:分式方程 分式方程是方程中的一种,且分母里含有未知数的(有理)方程叫做分式方程,等号两边至少有一个分母含有未知数。 考点2:一元一次不等式一元一次不等式的定义:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式。
注:
(1)首先要是一个不等式;
(2)不等式的两边都是整式;
(3)只含一个未知数,且未知数的最高次数是1。
一元一次不等式和一元一次方程概念的异同点:
相同点:二者都是只含有一个未知数,未知数的次数都是1,左、右两边都是整式.
不同点:一元一次不等式表示不等关系,一元一次方程表示相等关系.
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目

 ;
;

 ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sin37°≈
,sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)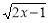 +2
+2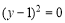 ,则
,则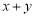 的值等于 ( )
的值等于 ( ) C. 2 D.
C. 2 D.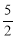
 ,若它们的众数为1,则这组数据的平均数为 .
,若它们的众数为1,则这组数据的平均数为 . 的解集是
的解集是 ,那么m的取值范围是 .
,那么m的取值范围是 . B.3×
B.3×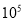 C.3×
C.3×