题目内容
在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式一定能成立的有
A.sinA=sinB B.a=c·sinB C.sin2A+cos2B=1 D.sinA=tanA·cosA
D.
【解析】
试题分析:如图,

∵sinA= ,sinB=
,sinB= ,cosA=
,cosA= ,tanA=
,tanA= ,
,
∴sinA≠sinB,所以A错误;
a=csinA,所以B错误;
sin2A+cos2A=( )2+(
)2+( )2=
)2= ,所以C错误.
,所以C错误.
∵tanAcosA=
 =
= =sinA,所以D正确;
=sinA,所以D正确;
故选D.
考点:1.互余两角三角函数的关系;2.锐角三角函数的定义.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 时,代数式
时,代数式 的值为
的值为 ,那么当
,那么当 时,这个代数式的值是( )
时,这个代数式的值是( ) B、
B、 C、
C、 D、
D、
 cm,点P从点A出发以1cm/s的速度移动到点B.点P出发 秒后,PA=2PC.
cm,点P从点A出发以1cm/s的速度移动到点B.点P出发 秒后,PA=2PC.
 )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有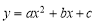 (
(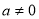 )的图象经过点A(-1,0)、点B(3,0)、点C(0,3).
)的图象经过点A(-1,0)、点B(3,0)、点C(0,3).
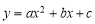 上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
 ;
;  ≤
≤ ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.