题目内容
(本小题满分6分)如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.

(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米?
(参考数据:sin67°≈ ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sin37°≈
,sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
【解析】
试题分析:(1)首先设CF=DE=x,根据三角函数将AE和BF分别用含x的代数式表示,根据AB=62米求出x的值;(2)根据三角函数分别求出BC和AD的长度,然后计算出BC+CD+AD的长度,然后与AB的长度进行比较.
试题解析:(1)设CF=x,则DE=x,EF=CD=20,则AE= =
= x,BF=
x,BF= =
= x,AB=BF+EF+AE=62
x,AB=BF+EF+AE=62
即 x+20+
x+20+ x=62 解得:x=24 即CD与AB的距离为24米
x=62 解得:x=24 即CD与AB的距离为24米
(2)根据题意可得:BC= =
= =40(米) AD=
=40(米) AD= =
= =26(米)
=26(米)
则AD+CD+BC=26+20+40=86(米) 86-62=24(米) 即多走24米.
考点:三角函数的应用.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
读取表格中的信息,解决问题.满足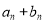 >1000的n可以取得的最小正整数是 .
>1000的n可以取得的最小正整数是 .
n=1 |
|
|
n=2 |
|
|
n=3 |
|
|
… | … | … |
 )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有 (x<0)的图象上,点B在反比例函数y=
(x<0)的图象上,点B在反比例函数y= (x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( )
(x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( )
 D.
D.
 的倒数是( )
的倒数是( ) B.
B. C.
C. D.
D. ;
;  ≤
≤ ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.






 ,再将x取一个喜欢的值代入计算.(6分)
,再将x取一个喜欢的值代入计算.(6分)
