题目内容
求证:等腰三角形两底角的平分线相等.
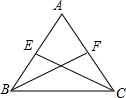 已知:△ABC中,AB=AC,BF,CE分别∠ABC,∠ACB的角平分线.
已知:△ABC中,AB=AC,BF,CE分别∠ABC,∠ACB的角平分线.求证:BF=CE,即等腰三角形的两底角的平分线相等
证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BF,CE分别∠ABC,∠ACB的角平分线,
∴∠BCE=∠CBF,
∵∠ABC=∠ACB,BC=BC,
∴△BCE≌△CBF,
∴BF=CE,即等腰三角形两底角的平分线相等.
分析:根据等腰三角形的两底角相等可得到∠ABC=∠ACB,再根据角平分线的性质可得到∠BCE=∠CBF,从而可利用ASA判定△BCE≌△CBF,由全等三角形的对应边相等即可证得结论.
点评:此题主要考查等腰三角形的性质以及全等三角形的判定与性质的综合运用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
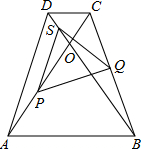 如图,等腰梯形ABCD中,CD∥AB,对角线ACBD相交于O,∠ACD=6O°,点S,P,Q分别是OD,OA,BC的中点,
如图,等腰梯形ABCD中,CD∥AB,对角线ACBD相交于O,∠ACD=6O°,点S,P,Q分别是OD,OA,BC的中点,