Question

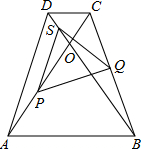如图，等腰梯形ABCD中，CD∥AB，对角线ACBD相交于O，∠ACD=6O°，点S，P，Q分别是OD，OA，BC的中点，
（1）求证：△PQS是等边三角形；
（2）若AB=5，CD=3，求△PQS的面积；
（3）若△PQS的面积与△AOD的面积的比是7：8，求梯形上、下两底的比CD：AB．

Answer 1

分析：（1）连接SC、PB，根据等腰三角形性质、直角三角形斜边中线、三角形中位线可判断出答案．
（2）根据等腰梯形的性质及∠AOD=120°可求出等边三角形的边长，从而可得出答案．
（3）设CD=a，AB=b（a＜b），根据题意表示出两面积的比，从而可得出答案．

解答：解：如图，连接SC、PB，
（1）证明：∵ABCD是等腰梯形，
∴AD=BC，
又∵AC、BD相交于O，
∴AO=BO，OC=OD，
∵∠ACD=60°，
∴△OCD和△OAB是等边三角形，
∵S是OD的中点，
∴CS⊥DO，
在RT△BSC中，Q为BC的中点，SQ是斜边BC的中线，
∴SQ=

1

2

BC．
同理BP⊥AC，在RT△BPC中，PQ=

1

2

BC，
又SP是△OAD的中位线，
∴SP=SQ=PQ，
∴△SPQ是等边三角形；

（2）∵AB=5，CD=3，
∴可得：CS=

3 3

2

，SB=

13

2

，
∴BC=7，
∴PS=PQ=SQ=

7

2

，
∴S_△PQS=

49 3

16

；

（3）设CD=a，AB=b（a＜b），
BC²=SC²+BS²=(

3

2

a)2+(b+

a

2

)2=a²+b²+ab，
∴S_△SPQ=

3

16

（a²+ab+b²），
又

S△PQS

S△AOD

=

7

8

，
∴8×

3

16

（a²+ab+b²）=7×

3

4

ab，
即2a²-5ab+2b²=0，
化简得

a

b

=

1

2

，
故

CD

AB

=

1

2

．

点评：本题考查面积及等积变换，难度较大，注意掌握等腰梯形及等边三角形的知识，基本知识的掌握是解答综合题的关键．