题目内容
已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G、∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.

(1)求证:△EGB是等腰三角形
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图(2))求此梯形的高.
【答案】
(1)证明见解析;(2)3 -2.
-2.
【解析】
试题分析:(1)根据题意,即可发现∠EBG=∠E=30°,从而证明结论;
(2)要使四边形ACDE成为以ED为底的梯形,则需BC⊥DE,即可求得∠BFD=30°.再根据30°的直角三角形的性质即可求解.
试题解析:(1)证明:∵∠C=∠EFB=90°,∠E=∠ABC=30°,
∴∠EBF=60°,
∴∠EBG=∠EBF-∠ABC=60°-30°=∠E.
∴GE=GB,
则△EGB是等腰三角形;
(2)解:要使四边形ACDE成为以ED为底的梯形,
则需BC⊥DE,即可求得∠BFD=30°.
设BC与DE的交点是H.
在直角三角形DFE中,∠FDH=60°,DF= DE=2,
DE=2,
在直角三角形DFH中,FH=DF•cos∠BFD=2×cos30°=2× =
= .
.
则CH=BC-BH=AB•cos∠ABC-(BF-FH)=2 -(2-
-(2- )=3
)=3 -2.
-2.
即此梯形的高是3 -2.
-2.
考点:1.梯形;2.等腰三角形的判定.

练习册系列答案
相关题目
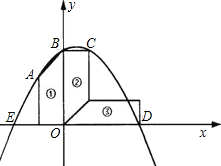 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.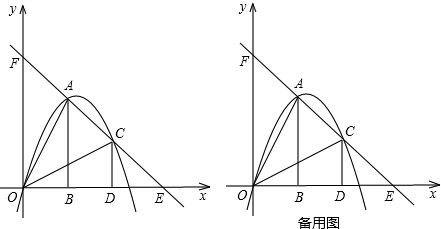
 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
