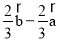题目内容
如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )

A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE= AB
AB
D.S△ABC=3S△DEF
C
【解析】
求出∠BDE=∠FEC=∠AFD=30°,求出∠DEF=∠DFE=∠EDF=60°,推出DF=DE=EF,即可得出等边三角形DEF,根据全等三角形性质推出三个三角形全等即可.求出AB=3BE,DE=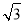 BE,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.
BE,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=∠A=60°,
∵DE⊥BC、EF⊥AC、FD⊥AB,
∴∠DEB=∠EFC=∠FDA=90°,
∴∠BDE=∠FEC=∠AFD=30°,
∴∠DEF=∠DFE=∠EDF=180°﹣90°﹣30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形,
在△ADF、△BED、△CFE中

∴△ADF≌△BED≌△CFE,
∴AD=BE=CF,
∵∠DEB=90°,∠BDE=30°,
∴BD=2BE,DE=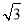 BE,
BE,
∴AB=3BE,
即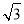 DE=AB,
DE=AB,
即DE=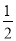 AB错误;
AB错误;
∵△ABC和△DEF是等边三角形,
∴△ABC∽△DEF,
∴S△ABC:S△DEF=(AB)2:(DE)2=(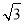 DE)2:DE2=3,
DE)2:DE2=3,
即只有选项C错误;选项A、B、D正确.
故选C.


练习册系列答案
相关题目



 B.
B. C.
C. D.
D.

 ,
, ,用
,用 、
、 表示向量
表示向量 正确的是( )
正确的是( ) B.
B. C.
C.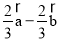 D.
D.