题目内容
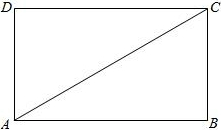 如图,矩形ABCD中,对角线AC=10,BC=5
如图,矩形ABCD中,对角线AC=10,BC=5| 3 |
考点:点与圆的位置关系
专题:计算题
分析:先利用勾股定理计算出AB=5,再根据点与圆的位置关系得到5<r<5
,由于⊙B和⊙D相切,则分类讨论:当⊙B和⊙D外切时,R+r=10,则r=10-R;
当⊙B和⊙D内切时,R-r=10,则r=R-10,然后根据r的范围确定对应的R的范围.
| 3 |
当⊙B和⊙D内切时,R-r=10,则r=R-10,然后根据r的范围确定对应的R的范围.
解答:解:在Rt△ABC中,∵AC=10,BC=5
,
∴AB=
=5,
∵A点在⊙B内部,C在⊙B外部,
∴5<r<5
,
当⊙B和⊙D外切时,R+r=10,则r=10-R,
∴5<10-R<5
,
∴10-5
<R<5;
当⊙B和⊙D内切时,R-r=10,则r=R-10,
∴5<R-10<5
,
∴15<R<10+5
.
| 3 |
∴AB=
| AC2-BC2 |
∵A点在⊙B内部,C在⊙B外部,
∴5<r<5
| 3 |
当⊙B和⊙D外切时,R+r=10,则r=10-R,
∴5<10-R<5
| 3 |
∴10-5
| 3 |
当⊙B和⊙D内切时,R-r=10,则r=R-10,
∴5<R-10<5
| 3 |
∴15<R<10+5
| 3 |
点评:本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则点P在圆外?d>r;点P在圆上?d=r点P在圆内?d<r.也考查了两圆相切的性质.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
要做甲乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为:30cm、50cm、60cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架一共有( )
| A、1种 | B、2种 | C、3种 | D、4种 |
 如图,AC=AD,BC=BD,连结CD交AB于点E,F是AB上一点,连结FC,FD,则图中的全等三角形共有( )
如图,AC=AD,BC=BD,连结CD交AB于点E,F是AB上一点,连结FC,FD,则图中的全等三角形共有( )| A、3对 | B、4对 | C、5对 | D、6对 |

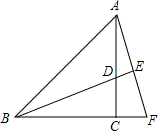 如图:△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC且交AC于点D,将△BCD绕点C顺时针旋转到△ACF的位置,并延长BD交AF于点E.
如图:△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC且交AC于点D,将△BCD绕点C顺时针旋转到△ACF的位置,并延长BD交AF于点E.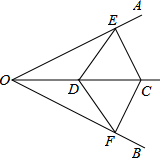 如图,CD是∠AOB平分线上的点,CE⊥OA于点E,CF⊥OB于点F,求证:∠CDE=∠CDF.
如图,CD是∠AOB平分线上的点,CE⊥OA于点E,CF⊥OB于点F,求证:∠CDE=∠CDF.