题目内容
11. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=6,BC=8.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=6,BC=8.(1)求CD的长;
(2)求△ADB的面积.
分析 (1)根据角平分线上的点到角的两边距离相等可得CD=DE,利用勾股定理列式求出AB,然后根据S△ABC=S△ACD+S△ABD列方程求解即可;
(2)求出DE=CD=3,由三角形面积公式即可得出结果.
解答 解:(1)∵∠ACB=90°,AD平分∠CAB,DE⊥AB于E,
∴CD=DE,
由勾股定理得,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵S△ABC=S△ACD+S△ABD,
∴$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AC×CD+$\frac{1}{2}$×AB×DE,
即$\frac{1}{2}$×6×8=$\frac{1}{2}$×6×CD+$\frac{1}{2}$×10×CD,
解得:CD=3;
(2)∵DE=CD=3,AB=10,
∴△ADB的面积=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×10×3=15.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,勾股定理,三角形面积的计算;利用三角形的面积列出方程求出CD是关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
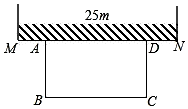 如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分),设矩形羊圈的面积为ym2,垂直于墙的一边长AB为x m.
如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分),设矩形羊圈的面积为ym2,垂直于墙的一边长AB为x m.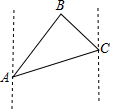 如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.74,$\sqrt{6}$≈2.45)
如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.74,$\sqrt{6}$≈2.45) 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.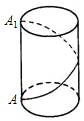 如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?
如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?