题目内容
设直角三角形的两条直角边长分别为a和b,斜边长为c
(1)已知a=12,b=5,求c;
(2)已知a=3,c=4,求b;
(3)已知c=10,b=9,求a.
(1)已知a=12,b=5,求c;
(2)已知a=3,c=4,求b;
(3)已知c=10,b=9,求a.
考点:勾股定理
专题:
分析:(1)根据c=
即可得出结论;
(2)根据b=
即可得出结论;
(3)根据a=
即可得出结论.
| a2+b2 |
(2)根据b=
| c2-a2 |
(3)根据a=
| c2-b2 |
解答:
解:(1)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=12,b=5,
∴c=
=
=13;
(2)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=3,c=4,
∴b=
=
=
;
(3)∵直角三角形的两条直角边长分别为a和b,斜边长为c,c=10,b=9,
∴a=
=
=
.
∴c=
| a2+b2 |
| 122+52 |
(2)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=3,c=4,
∴b=
| c2-a2 |
| 42-32 |
| 7 |
(3)∵直角三角形的两条直角边长分别为a和b,斜边长为c,c=10,b=9,
∴a=
| c2-b2 |
| 102-92 |
| 19 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
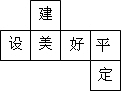 2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )
2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、好 | C、平 | D、定 |
若不等式(a+1)x>2的解集为x<
,则a的取值范围是( )
| 2 |
| a+1 |
| A、a<1 | B、a>1 |
| C、a<-1 | D、a>-1 |
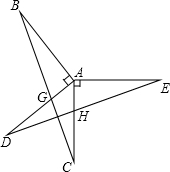 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H. 如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?
如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?