Question

7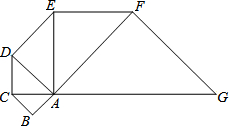．已知△ABC是腰长为1的等腰直角三角形，以Rt△ABC为斜边AC为直角边，画第2个等腰直角三角形ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，以此类推，第n个等腰直角三角形的面积是2^n-2．

Answer 1

分析 将前4个等腰三角形的面积计算出来，然后找出规律即可求出答案．

解答 解：由勾股定理可知：AC²=2，AD²=4，AE²=8，AF²=16，
故第n个等腰三角形的斜边的平方为：2ⁿ，
设等腰三角形的直角边长为a；斜边长为c，
∴由勾股定理可知：c²=2a²
由三角形面积公式可知：$\frac{1}{2}$a²=$\frac{1}{4}$c²，
∴第n个等腰三角形的面积为：$\frac{1}{4}$×2ⁿ=2^n-2
故答案为：2^n-2

点评 本题考查规律问题，解题的关键是根据前4个等腰三角形的斜边找出规律，本题属于中等题型．