题目内容
8.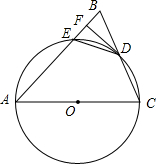 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.(1)求证:直线DF与⊙O相切;
(2)求证:△BED∽△BCA;
(3)若AE=7,BC=6,求AC的长.
分析 (1)连接OD,利用AB=AC,OD=OC,证得OD∥AD,易证DF⊥OD,故DF为⊙O的切线;
(2)根据圆内接四边形的性质得到∠BED=∠C,然后根据相似三角形的判定定理即可得到结论;
(3)证得△BED∽△BCA,求得BE,利用AC=AB=AE+BE求得答案即可.
解答 (1)证明:如图,连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)证明:∵∠BED=∠C,∠B=∠B,
∴△BED∽△BCA;
(3)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴$\frac{BD}{AB}=\frac{BE}{BC}$,
∵OD∥AB,AO=CO,
∴BD=CD=$\frac{1}{2}$BC=3,
又∵AE=7,
∴$\frac{3}{7+BE}=\frac{BE}{6}$,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.
点评 此题考查了切线的判定,三角形相似的判定与性质,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
18.计算6÷(-2)的结果是( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | -12 |
16.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )
| A. | $\left\{{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{8x+3=y}\\{7x-4=y}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{y-8x=3}\\{y-7x=4}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{8x-y=3}\\{7x-y=4}\end{array}}\right.$ |
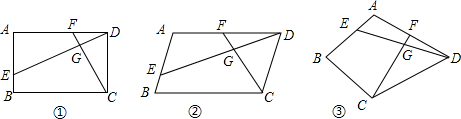 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.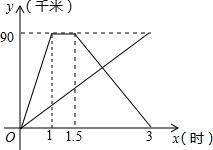 甲、乙两个人同时从相距90千米的A地前往B点,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们 离A地的距离y(千米)与时间x(时)之间的函数关系图象.
甲、乙两个人同时从相距90千米的A地前往B点,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们 离A地的距离y(千米)与时间x(时)之间的函数关系图象.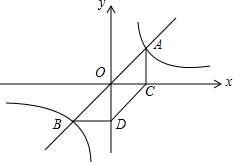 如图,一过原点的直线y=mx(m>0)与反比例函数$y=\frac{k}{x}$(k>0)的图象交于A、B两点,过A、B两点分别向x轴、y轴作垂线,垂足分别为C、D两点,连接CD.
如图,一过原点的直线y=mx(m>0)与反比例函数$y=\frac{k}{x}$(k>0)的图象交于A、B两点,过A、B两点分别向x轴、y轴作垂线,垂足分别为C、D两点,连接CD. 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论: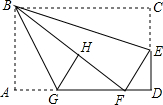 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: