题目内容
6.如图(1),路灯灯柱AB,CD之间有一棵大树MN,点B、N、D在一条水平线上,大树在灯泡A的照射下影子恰好到点D,在灯泡C的照射下影子恰好到点B.(1)若AB=12米,CD=8米,BD=14米,求大树MN的高度.
(2)若AB=12米,CD=8米,不知道BD的长,树高能否求得?若能求得,树高是多少?若不能求得,请说明理由.
(3)若AB=a米,CD=b米,求大树MN的高度.
(4)若点B、N、D在一条斜线上,如图(2),能否用(3)得到的结果求大树MN的高度?
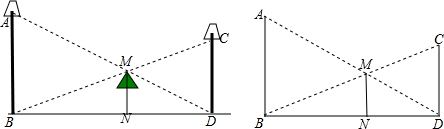
分析 (1)利用相似三角形的判定方法,可判断△DMN∽△DAB,则$\frac{MN}{AB}$=$\frac{DN}{DB}$①,再判断△BMN∽△BCD得到$\frac{MN}{CD}$=$\frac{BN}{BD}$②,然后把两式相加易MN=$\frac{AB•CD}{AB+CD}$,最后把AB和CD的值代入计算即可;
(2)由(1)得MN=$\frac{AB•CD}{AB+CD}$,于是可判断MN的长只与AB和CD有关,MN=$\frac{24}{5}$;
(3)由(1)得MN=$\frac{ab}{a+b}$(m);
(4)能用(3)得到的结果求大树MN的高度.
解答 解:(1)∵MN∥AB,
∴△DMN∽△DAB,
∴$\frac{MN}{AB}$=$\frac{DN}{DB}$①,
∵MN∥CD,
∴△BMN∽△BCD,
∴$\frac{MN}{CD}$=$\frac{BN}{BD}$②,
①+②得$\frac{MN}{AB}$+$\frac{MN}{CD}$=$\frac{DN+BN}{BD}$=1,
∴MN=$\frac{AB•CD}{AB+CD}$=$\frac{12×8}{12+8}$=$\frac{24}{5}$(m);
(2)能.
由(1)得MN=$\frac{AB•CD}{AB+CD}$,
∴MN的长只与AB和CD有关,MN=$\frac{24}{5}$;
(3)由(1)得MN=$\frac{AB•CD}{AB+CD}$=$\frac{ab}{a+b}$(m);
(4)能用(3)得到的结果求大树MN的高度.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,然后利用对应边成比例求相应线段的长.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,D为△ABC的边AC上一点,满足AD=2CD,G为BD的中点,AG的延长线交BC于点E.求BE:EC的值.
如图,D为△ABC的边AC上一点,满足AD=2CD,G为BD的中点,AG的延长线交BC于点E.求BE:EC的值.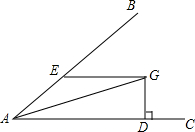 已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG.
已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG.