题目内容
4. 如图,正方形ABCD,点P为对角线AC上一个动点,Q为CD边上一点,且∠BPQ=90°.
如图,正方形ABCD,点P为对角线AC上一个动点,Q为CD边上一点,且∠BPQ=90°.(1)求证:PB=PQ;
(2)若BC+CQ=8,求四边形BCQP的面积;
(3)设AP=x,ABCD的面积为y,且CQ=2,求y与x的函数关系式.
分析 (1)如图1中,作PE⊥BC于E,PF⊥CD于F.只要证明△PEB≌△PFQ即可解决问题;
(2)只要证明S四边形BCQP=S四边形CEPF即可解决问题;
(3)如图2,过P做EF∥AD分别交AB和CD于E、F.易知AE=PE=$\frac{\sqrt{2}}{2}$x,由△BPE≌△PQF,推出EP=AE=QF=$\frac{\sqrt{2}}{2}$x,由BE=CF=2+$\frac{\sqrt{2}}{2}$x,推出AB=2+$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$x=2+$\sqrt{2}$x,由此即可解决问题;
解答 (1)证明:如图1中,作PE⊥BC于E,PF⊥CD于F.
∵四边形ABCD是正方形,
∴∠ACD=∠ACB,∵PE⊥BC于E,PF⊥CD于F,
∴PE=PF,
∵∠PEC=∠PFC=∠ECF=90°,
∴四边形PECF是矩形,∵PE=PF,
∴四边形PECF是正方形,
∴∠EPF=∠BPQ=90°,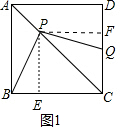
∴∠BPE=∠QPF,∵∠PEB=∠PFQ=90°,
∴△PEB≌△PFQ,
∴PB=PQ.
(2)解:如图1中,由(1)可知△BPE≌△PQF,四边形PECF是正方形,
∴BE=FQ,CE=CF,S△BPE=S△PQF,
∵BC+CQ=8,
∴EC+FC=BC+CQ=8,
∴CE=CF=4,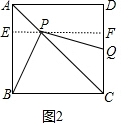
又∵S△BPE=S△PQF,
∴S四边形BCQP=S四边形CEPF=16.
(3)解:如图2,过P做EF∥AD分别交AB和CD于E、F.
∵AP=x,
∴AE=PE=$\frac{\sqrt{2}}{2}$x,
∵△BPE≌△PQF,
∴EP=AE=QF=$\frac{\sqrt{2}}{2}$x,
∵BE=CF=2+$\frac{\sqrt{2}}{2}$x,
∴AB=2+$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$x=2+$\sqrt{2}$x,
∴y=(2+$\sqrt{2}$x)2=2x2+4$\sqrt{2}$x+4.
点评 本题考查四边形综合题、全等三角形的判定和性质、正方形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案 为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:| 组别 | 次数x | 频数(人数) |
| 第1组 | 80≤x<100 | 6 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 18 |
| 第5组 | 160≤x<180 | 6 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?
 如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上.
如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上. 如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为( )