题目内容
8.等腰三角形的一腰上的高与另一腰的夹角是34°,则它的底角的度数是62°或28°°.分析 先知三角形有两种情况(1)(2),求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度数.
解答 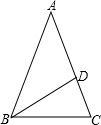 解:有两种情况;
解:有两种情况;
(1)如图当△ABC是锐角三角形时,BD⊥AC于D,
则∠ADB=90°,
已知∠ABD=34°,
∴∠A=90°-34°=56°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$×(180°-56°)=62°;
(2)如图,当△EFG是钝角三角形时,FH⊥EG于H,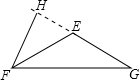 则∠FHE=90°,
则∠FHE=90°,
已知∠HFE=34°,
∴∠HEF=90°-34°=56°,
∴∠FEG=180°-56°=124°,
∵EF=EG,
∴∠EFG=∠G=$\frac{1}{2}$×(180°-124°)=28°,
∴它的底角的度数是62°或28°.
故答案为:62°或28°.
点评 本题考查了三角形有关高问题有两种情况的理解和掌握,能否利用三角形的内角和定理和等腰三角形的性质,知三角形的一个角能否求其它两角.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.若x:y=5:2,则(x+y):y的值是( )
| A. | 2:5 | B. | 7:2 | C. | 2:7 | D. | 3:2 |
19.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角等于( )
| A. | 160° | B. | 150° | C. | 120° | D. | 60° |
13.在-0.1010010001,-$\sqrt{7}$,$\frac{3}{7}$,-$\frac{π}{3}$,$\root{3}{8}$,0这六个数中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图:已知两直线l1和l2相交于点A(4,3),且OA=OB,则点B的坐标为(0,-5).
如图:已知两直线l1和l2相交于点A(4,3),且OA=OB,则点B的坐标为(0,-5).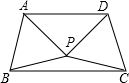 如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,下列四个结论:
如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,下列四个结论: