题目内容
8．
如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，且BC∥QR，则∠AOQ的度数为（ ）| A． | 45° | B． | 60° | C． | 75° | D． | 90° |
分析 连结OD，根据等边三角形性质得PQ=PR=QR，则∠POQ=$\frac{1}{3}$×360°=120°，根据圆内接等边三角形的性质有OP⊥QR，而BC∥QR，所以OP⊥BC，根据四边形ABCD是⊙O的内接正方形，则OP⊥AD，∠AOD=90°，然后根据垂径定理可得∠AOP=∠DOP=45°，再利用∠AOQ=∠POQ-∠AOP计算即可．
解答 解：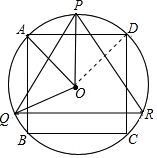
连结OD，
∵△PQR是⊙O的内接正三角形，
∴PQ=PR=QR，
∴∠POQ=$\frac{1}{3}$×360°=120°，OP⊥QR，
∵BC∥QR，
∴OP⊥BC，
∵四边形ABCD是⊙O的内接正方形，
∴OP⊥AD，∠AOD=90°，
∴$\widehat{AP}$=$\widehat{DP}$，
∴∠AOP=∠DOP，
∴∠AOP=$\frac{1}{2}$×90°=45°，
∴∠AOQ=∠POQ-∠AOP=75°．
故选：C．
点评 本题考查了正多边形与圆的关系、圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图△ABC中，∠ACB=90°，AC+BC=8，分别以AB、AC、BC为半径作半圆，若记图中阴影部分的面积为y，AC为x，则下列y关于x的图象中正确的是（ ）
如图，等腰三角形ABC的底边BC长为4，面积是12，腰AB的垂直平分线EF分别交AB，AC于点E、F，若点D为底边BC的中点，点M为线段EF上一动点，则△BDM的周长的最小值为8．
如图，将100张长为30cm、宽相等的长方形白纸，按如图所示的方法粘起来，粘合的部分宽为3cm，求粘合后总长度．