题目内容
8.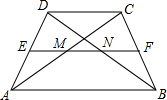 如图,在四边形ABCD中,E,F分别是边AD,BC的中点,且EF∥AB,与对角线AC,BD分别交于M,N两点,若EF=20cm,MN=8cm,求AB的长.
如图,在四边形ABCD中,E,F分别是边AD,BC的中点,且EF∥AB,与对角线AC,BD分别交于M,N两点,若EF=20cm,MN=8cm,求AB的长.
分析 根据题意证明EF∥CD,根据三角形中位线定理证明EM=NF,求出EN的长,根据三角形中位线定理求出AB的长.
解答 解:∵E,F分别是边AD,BC的中点,EF∥AB,
∴EF∥CD,
∴EM=$\frac{1}{2}$CD,NF=$\frac{1}{2}$CD,
∴EM=NF=$\frac{1}{2}$(EF-MN)=6,
∴EN=EM+MN=14,
∵EF∥AB,E是边AD的中点,
∴AB=2EN=28cm.
点评 本题考查的是梯形的中位线定理和三角形的中位线定理,掌握梯形的中位线平行于两底,且等于两底和的一半是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某商店出售一种商品,有以下几种方案,调价后价格最低的方案是( )
| A. | 先提价10%,再降价10% | B. | 先降价10%,再提价10% | ||
| C. | 先提价15%,再降价15% | D. | 先提价20%,再降价20% |
18.一次实验中,总数为100,共甲、乙两项.甲项出现的频数为30,则乙项出现的频率为( )
| A. | 0.7 | B. | 0.3 | C. | 30 | D. | 70 |
 如图,在△ABC中,∠ACB=90°,∠ACD=∠B,求证:CD⊥AB.
如图,在△ABC中,∠ACB=90°,∠ACD=∠B,求证:CD⊥AB. 作图题:点A为∠ABC的边AB上的一点,过点A作直线EF∥BC(用尺规作图,不写作法,保留作图痕迹).
作图题:点A为∠ABC的边AB上的一点,过点A作直线EF∥BC(用尺规作图,不写作法,保留作图痕迹).