题目内容
17．
如图，在△ABC中，点D，E分别是AB，AC边的中点，沿DE折叠，点A落在BC边上的点P处，若∠B=46°，则∠BPD的度数为（ ）| A． | 44° | B． | 46° | C． | 54° | D． | 56° |
分析 由折叠的性质可知AD=PD，再根据中点的性质得AD=BD=PD，根据等腰三角形的性质，可得∠DPB的度数．
解答 解：由折叠的性质知，AD=PD，
∵点D为AB边的中点，
∴AD=BD，
∴BD=PD，
∴∠DPB=∠B=46°，
故选：B．
点评 本题考查了翻折变换的知识，解答本题的关键是根据翻折变换的性质：翻折前后对应边相等，得出△BDP是等腰三角形．
练习册系列答案
相关题目
7．下列各组中的四条线段成比例的是（ ）
| A． | 1cm、2cm、20cm、30cm | B． | 1cm、2cm、3cm、4cm | ||
| C． | 5cm、10cm、10cm、20cm | D． | 4cm、2cm、1cm、3cm |
如图，AB∥DG，∠1+∠2=180°，
5．
一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时候到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（ ）
一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时候到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（ ）| A． | 80海里 | B． | 70海里 | C． | 60海里 | D． | 40海里 |
12．
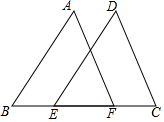如图，点E，F在BC上，BE=CF，∠B=∠C，若要证明△ABF≌△DCE，则还需要补充的条件不可能是（ ）
如图，点E，F在BC上，BE=CF，∠B=∠C，若要证明△ABF≌△DCE，则还需要补充的条件不可能是（ ）| A． | ∠A=∠D | B． | ∠AFB=∠DEC | C． | AF=DE | D． | AB=CD |
2．直角三角形的两直角边长分别为6和8，则斜边上的中线长是（ ）
| A． | 10 | B． | 2.5 | C． | 5 | D． | 8 |
9．下列各组数：①-1与+1；②+（+1）与-1；③-（-2）与+（-2）；④-（-$\frac{1}{2}$）与+（+$\frac{1}{2}$）：⑤+[-（+1）]与-[+（-1）]；⑥-（+2）与-（-2），其中，互为相反数的有（ ）
| A． | 6组 | B． | 5组 | C． | 4组 | D． | 3组 |
6．下列四个图形中，是轴对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
7．下列各式一定成立的是（ ）
| A． | 3（x+8）=3x+8 | B． | -（x-6）=-x-6 | ||
| C． | -a+b-c+d=-a+（b+c-d） | D． | -（a-b+c）+d=-a+b-c+d |