题目内容
先化简再求值:[(xy+3)(3-xy)-9(xy+1)2]÷2xy,其中x=-2,y=
.
| 1 |
| 2 |
考点:整式的混合运算—化简求值
专题:计算题
分析:原式中括号中第一项利用平方差公式化简,第二项利用完全平方公式展开,合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
解答:解:原式=(9-x2y2-9x2y2-18xy-9)÷2xy
=-5xy-9,
当x=-2,y=
时,原式=5-9=-4.
=-5xy-9,
当x=-2,y=
| 1 |
| 2 |
点评:此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
在下列各组数据中,不能作为直角三角形的三边边长的是( )
| A、5,12,13 |
| B、6,8,10 |
| C、7,24,25 |
| D、8,15,16 |
 如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是( )
如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是( )| A、|b|>|a| |
| B、a-b<0 |
| C、a+b<0 |
| D、ab<0 |
已知等腰三角形的周长为16,若设腰长为x,则x的取值范围是( )
| A、4≤x≤8 | ||
| B、4<x<8 | ||
C、
| ||
D、
|
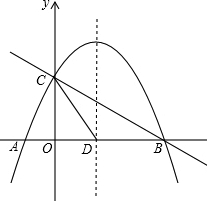 如图,抛物线y=-
如图,抛物线y=-